CFD Analysis of Solar Air Heater Using V-Shaped Artificial Roughness to Attain Heat Transfer Enhancement

The influx of Solar energy is the primary and predominant form of energy source on our planet. In the absence of an atmospheric layer, when the Sun is located at a distance of 1.495×10¹¹ meters from Earth and has a diameter of 1.39×10⁹ meters, its surface area perpendicular to its beams would generate an estimated power output of approximately 1353 watts. The planet receives solar energy at a rate of 170 trillion kilowatt-hours (kWh). Roughly 30% of the total energy is dissipated into the surrounding space through the process of reflection [1]. About 47% of the energy is transformed into low-temperature thermal energy. The Biosphere utilizes approximately 23% of the energy for the purposes of evaporation and precipitation. A small fraction, less than 0.5%, is captured and utilized through wind, wave action, and plant photosynthesis.

Solar energy systems consist of a collection of individual components. The solar air heater uses this solar energy for heating air which is then used for multiple purposes like food drying etc. [2]. The commercial design of the solar air heater is shown in Figure 1. The solar air radiators are responsible for facilitating the heat transfer between the absorber and the fluid in both directions, making them an essential component in these systems [3].

1.png

Figure 1. The general design of a solar air heater [4]

Typically, modifications are implemented on solar air purifiers with the objective of directly impacting their effectiveness. The increasing advancement of human civilization has led to a greater reliance on natural resources to meet its essential needs. The dehydration of fruits and vegetables, such as grapes, pawpaw, and pepper, necessitates the utilization of fuel derived from natural resources through the process of combustion. Solar energy air radiators are a type of heat exchanger that transforms the thermal energy of the transport medium into solar radiation. Solar air heaters are essential components of solar systems. Solar air heaters, although they generate lower temperatures compared to other sun thermal air heaters, possess advantages such as a more straightforward design, reduced maintenance needs, and cost-efficiency. The advancement of solar air purifiers equipped with thermal storage technology has optimized the utilization of solar energy, resulting in enhanced efficiency and cost reduction.

Saini and Saini [5] conducted an experimental investigation on solar air heaters incorporated with arc-shaped roughness. The effect of geometric design parameters i.e. arc angle and e/D_h ratio is evaluated for HTC value and friction factor. The experimental analysis was conducted for Re number varying from 1200 to 17000. The experimental findings have shown an augmentation of Nusselt number (Nu) by nearly 3.8 times at an arc angle of 0.33 and d/D_h value of 0.042. The frictional factor is found to be minimal.

Saini and Verma [6] studied solar air collectors by changing geometric design parameters e/D_h and p/e (geometric designs). The thermal analysis was completed for an input number (temperature derivative ratio) varied between 1900 to 12400. The parameters for this analysis consist of a/b (0.018-0.037), and l/w (8-12) among other factors. Design parameters correlate in the following manner: Nusselt number and friction factor are found. The highest value, which is obtained for p/e = 10, is the one for which the friction factor is 0.0289. The experimentally validated computational fluid dynamics model used by Singh et al. [7] covers rib configurations of different geometries in down-flow systems. This work focuses on the effect of various rib geometries on thermal characteristics in S.A.Hs. This study also shows that a half-trapezoidal rib design offers the maximum enhancement in thermal efficiency and that the efficiency is 17% higher. Quarter circulars also do well and offer thermal performance enhancement of 16 percent in this case. Apart from the thermal analysis, the paper presents useful insights in relation to the frictional losses. Concerning the static pressure distribution, it was pointed out that all the quarter-circular rib types analyzed reveal about 10% lower friction than trapezoidal ribs, which was seen as a proper compromise between thermal enhancement and flow resistance.

Furthermore, the study also focuses on exergy recovery to measure the efficiency of the mentioned rib designs. The investigation on trapezoidal and circular ribs PAHs reveals that the ribbed surface enhances the exergy entity by 35% compared with a flat smooth SAH. This important result shows that these configurations of ribs can improve the efficiency of the entire system. Thianpong et al. [8] conducted experimental investigations on solar air heaters by incorporating isosceles triangular ribs. The arrangement of ribs is done in staggered type and in-plane type for Re values ranging from 5500 to 22000. The analysis is conducted with varying hydraulic diameters to pipe diameters varying between 0.0733 and 0.147. The analysis is conducted for both symmetric and asymmetric rib configurations. From the analysis, it was found that in-line rib design has shown a higher Nusselt number and friction factor as compared to staggered design configuration. The maximum thermal performance of SAH is observed for an e/D_h value of 0.145.

Kazemi Moghadam et al. [9] have investigated a solar air heater having arc-shaped ribs newly designed to investigate the thermal performance of the augmenter by numerical analysis. The heat transfer characteristics of the augmenter are investigated comprehensively. For Reynolds numbers 6000 and 12000, the effects of different design factors involving cross-sectional shapes, spacing, aspect ratio, and rib pitch on thermal performance are investigated. The tests suggest that the quadrangular-shaped ribs provide the greatest coefficient of performance when compared to other shapes. Moreover, the study reveals that when the rib pitch is set to 40 mm and the aspect ratio to 0.5, thermal performance is improved. In particular, it became possible to establish that the spacings between the ribs influenced the solar air heater’s thermal efficiency to the least extent. These correlations are expected to help in the better design and better performance of the solar air heaters in practical application. Kumar et al. [10] performed an investigation of SAH by incorporating W-shaped ribs on an absorber plate. The thermal energy was selectively transferred to the absorber plate, while the remaining surfaces were maintained at adiabatic conditions. The rectangular duct was measured to have an aspect ratio of 8:1. The analysis was conducted for Re value ranging from 2800 to 15000, for e/D_h value ranging from .0168 to .0338, and AOA varying from 30° to 75°. The maximum heat transfer enhancement is attained for an e/D_h value of 0.035.

Chompookham et al. [11] steered an experimental investigation on the rectangular duct of SAH. The channel geometry has a P/H ratio of 1.33, e/H ratio of 0.2. The analysis was conducted to determine the thermal characteristics of the fully developed turbulent fluid. The thermal boundary conditions are applied on the upper face of the duct and on the absorber surface. The subsequent analysis was conducted by incorporating WVG vortex generators at the inlet zone of the duct. The application of WVG vortex generators has shown a 5.8% enhancement of HTC value at an AOA value of 60°.

The efficacy of a two-phase integrated absorption cooler was investigated by Farhan [12] by combining experimental and theoretical approaches. The proof of DPSAH by Metrologic hour data collected through December 2016 and January 2017 was specifically for the Baghdad region in Iraq. The research showed that the air equivalent factor of the framework surged when the airflow velocity increased through the collector. This caused a rapid decrease in the temperature of the air leaving the system. It, further, helps with the primary output of electricity and improves the recovery use to be more efficient as well. At 12 PM, the temperature and speed reading on the air outlet were approximately 3 App degrees and a flow rate of 0.01 cubic meters per second respectively. The degree of value for the Swirl-Trapping researchers was increased by 6% when the DPSAH design was used in the place of single pass design configuration (SPSAH) at constant airflow velocity.

Momin et al. [13] conducted an experimental investigation of SAH incorporated with V-shaped ribs. The V-shaped ribs are placed at the bottom of SAH and the Re number is varied from 2500 to 18500, with e/D_h value ranging from 0.02 to 0.034, and AOA value ranging from 30° to 90°. The increase of friction factor and HTC values are determined and the effect of e/D_h on friction factor, HTC is established and compared with roughened surface.

Matheswaran et al. [14] conducted thermal analysis on double-pass SAH using numerical techniques. The energy and exergy analysis are conducted for SAH with varying artificial roughness. The numerical results obtained are validated with the experimental test results available in the literature. The results of exergy and energy analysis obtained from double-pass SAH are compared with the results obtained from single-pass SAH. The results have shown that double-pass SAH has better performance as compared to single-pass SAH by 8% (exergy analysis) and 7.1% (energy analysis).

Matheswaran et al. [15] conducted experimental testing on single pas SAH mass flow rate ranging from 0.002 to 0.023 Kg/s. The energy and exergy analysis are conducted for different pitch ratios ranging from 0.435 to 0.869. The research findings have shown that exergy efficiency increases by 21.2% by varying pitch ratios and energy efficiency increases by 22.4%. The exergy efficiency is found to be affected by different parameters i.e. mass flow rate, X/D_h, and Y/D_h ratios. The optimal performance is attained at (X/D_h = 1.739), the span-wise pitch ratio (Y/D_h = 0.869), diameter ratio (D_j/D_h = 0.065), and mass flow rate of 0.0035 Kg/s. The correlations between Re number and jet plate design variables are established. Panda and Kumar [16] analyze the use of artificial roughness on the surface of the solar air heaters expose to heat to increase the heat transfer rate of the fluid through the air duct. The study also points out that artificial roughness is an effective mechanism when it comes to enhancing thermal performance. The authors explore different roughness geometries and their effect on both heat transfer and friction in the solar air heater studied. His review focuses on the factors that various geometries of the elements applied as artificial roughness must have to enhance the thermal and thermo-hydraulic characteristics of the solar air heater ducts. Much can be learned from this work, especially the best strategies to employ in the design of solar thermal systems towards energy efficiency. Saxena et al. [17] presented various types of roughness geometries in detail to increase the SAH efficiency with artificial roughness. The study presents a systematic comparison between various rib shapes as well as their heat transfer coefficients. Therefore, this study finds that using different types of rib forms in the SAHs can offer great potential benefits related to optimized thermal enhancement, which is highly informative for various design strategies applied in solar thermal systems. Kumar et al. [18] compared the results of an experimental investigation carried out for the efficiency of absorber plates with and without rib roughness. Both configurations are black painted with dispersed graphene nanoparticles into the paint. The researchers used a numerical and experimental approach to evaluate how surface roughness affects friction factors and heat transfer characteristics. The findings also suggest that smooth plates are on average up to 12% more efficient at converting heat into useful work than rough plates, with overall efficiencies of 4.82 and 4.46 respectively. This research therefore establishes that surface characteristics play a crucial role in the utilization of solar thermal systems. Esmaeili Shayan et al. [19] investigated the performance impact of different geometrical positions of the rectangular S-shaped artificial roughness placed inline and staggered in solar air heaters. This research proposes to validate the improvement realized in thermo-hydraulic performance utilizing different roughness configurations. Such characteristics as the length and height of the roughness elements, and the constant size of intervals between them fall under key parameters considered. The Reynolds number was set from 3,000 to 10,000 and the pitch was changed for the inline positions, while the length ratios were changed for the staggered ones. The maximal values of the Nusselt number, which characterizes heat transfer intensity, were noted at the given pitch-to-height ratio for both cases, and they were 4.87 and 4.2 times higher than those for a smooth tube.

The technological potential of solar air heaters (SAH) has been explored in numerous studies. However, there is no comprehensive understanding of the impact of rib angles on the thermal-hydraulic performance of the SAH. So far, research has been mainly oriented to the effect of rib shapes and configurations on heat transport and the characteristics of fluid flow. Nevertheless, the exact role of rib angles, mainly V-shaped, on the general behavior of these structures is still largely unknown. This is the aspect that needs to be kept in mind for designing and enhancing the SAH efficiency, especially its thermal-hydraulic performance. For this study, it is hypothesized that changing the angles of V-shaped ribs on the solar-air-heater will play a noteworthy part in the thermal-hydraulic efficiency of the system. Particularly, it is predicted that various rib angles would produce differing amounts of heat transfer improvements and friction factors, which necessarily affect the overall THPF of the solar air heater. The Research Questions considered in this study are:

1. The role of varying rib angles in V-shaped ribs in the heat transfer properties of a solar air heater:

2. How does the angle of the rib affect the friction factor in a solar air heater?

3. How do the different rib angles contribute to the thermal-hydraulic performance factor (THPF) of a solar air heater?

4. What is the best possible value of the rib angle that maximizes the thermal-hydraulic performance of the solar air heater?

The objective of the present study is to perform CFD simulation using ANSYS CFX software by varying rib angles. The roughness profile used for analysis is V-shaped with varying rib angles and keeping the depth constant for all analyses whereas roughness angles are varied from 60°, 90°, and 120°. Nusselt number and friction factor are calculated at various Reynolds numbers. Using these two parameters THPF is computed.

The way that section titles and other headings are displayed in these instructions, is meant to be followed in your paper. Validation and Grid Independence: for validation, the CFD analysis is conducted on the solar air heater having smooth duct i.e. without any artificial roughness. Selection of the best grid size is very important to achieve accurate results. Hence, grid independence tests were performed to predict appropriate grid dimensions to carry out the numerical simulations over a range of Reynolds numbers. The grid independence test was conducted at Re = 3800. In the grid independence test, the total number of grids was increased till the difference in results between two consecutive grid sizes became negligible. At this moment, the grid size corresponding to the second last case of the grid independence test was considered to be the best one and it was used for further simulations. The temperature distribution plot is shown in Figure 9.

9.png

Figure 9. Temperature distribution plot

Separate grid independence tests were conducted for different geometries. From the grid independence table (Table 3) the results of mean temperature remain concurrent and therefore for our analysis, we have selected 79685 number of elements.

Table 3. Grid independence evaluation

Table 4 shows the percentage deviation in Nusselt number for smooth duct between Dittus-Boelter correlation results and CFD results and the graphic representation is shown in Figure 10.

Table 4. Percentage deviation in Nusselt number for smooth duct between Dittus-Boelter correlation results and CFD results

The maximum deviation in Nusselt number (Nu) is 4.119% which shows a good agreement between the correlations and CFD values ensuring the accuracy of the analysis. After conducting CFD analysis on ANSYS CFX the contour plots of pressure, temperature, and turbulence kinetic energy are plotted. In the next stage, CFD simulation is carried out on rectangular ducts with varying rib angles. The depth is kept constant at 3 mm, and rib angles are varied from 600, 900, and 1200. Nusselt number, friction factor is determined which is used to calculate THPF.

10.png

Figure 10. Nusselt number VS. Reynolds number

3.1 Case 1: CFD analysis with 600 rib angles

The temperature plot, as shown in Figure 11, produced with a roughness height of 3 mm and an angle of 600 at a Reynolds number of 3900 exhibited non-uniform temperature change over the length of the duct. The maximum temperature is 318 Kelvin, while the minimum temperature is 300 Kelvin.

11.png

Figure 11. Temperature plot at 3900 Reynolds number

The pressure at the intake is initially greater and gradually decreases as it progresses towards the outlet, as seen in Figure 12. The pressure is elevated in the intercostal spaces directed toward the intake face, as shown by the red coloration.

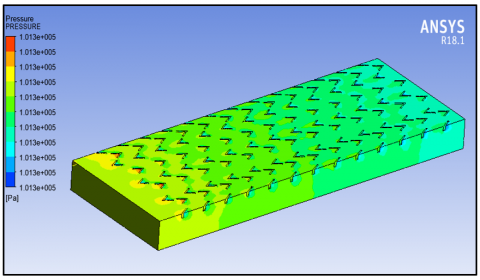
Figure 12. Pressure plot at 3900 Reynolds number

The velocity plot shown in Figure 13 illustrates a decrease in velocity between ribs, as seen by the light blue and dark blue colors along the rib row. The highest velocity achieved is located at the outlet area, shown by the dark red hue. The velocity disparity between the absorber face and rib face at the bottom results in the formation of vortices. Turbulent flow enhances the rate of heat transfer. The greatest velocity achieved is 2.12 m/s, while the smallest velocity achieved is 0.14 m/s.

13.png

Figure 13. Velocity plot at 3900 Reynolds number

3.2 Case 2: CFD analysis with 900 rib angles

The plot in Figure 14 displays the results obtained with a roughness height of 3 mm, specifically at a rib angle of 900. Below are the temperature plot, pressure plot, and velocity plot.

14.png

Figure 14. Temperature plot at 3900 Reynolds number

The temperature plot shows an uneven distribution of temperature over the length of the duct. The temperature gradient is seen to be higher in the vicinity of the ribs, as shown by the green contours, and decreases as we approach farther away from the ribs, as indicated by the light blue contours. The temperature exhibits variation in both the horizontal and vertical directions. The maximum temperature is 318K and the minimum temperature is 300K.

The pressure plot indicates the formation of a high-pressure region at the entrance section, with a non-uniform decrease in pressure as we go towards the duct outlet, as seen in Figure 15 below.

15.png

Figure 15. Pressure plot at 3900 Reynolds number

The air velocity experiences a significant decrease in proximity to the rough surface, but it gradually increases as we go farther away from it. This trend is visually represented by the light green and yellow colors in Figure 16.

16.png

Figure 16. Velocity plot at 3900 Reynolds number

3.3 Case 3: CFD analysis with 1200 rib angles

In this section results obtained from a roughness height of 3 mm are plotted at 1200 rib angle. The temperature plot, pressure plot, and velocity plot are given in Figure 17.

17.png

Figure 17. Temperature plot at 3900 Reynolds number

The temperature plot as shown in Figure 17 obtained for roughness height 3 mm and 1200 angle at 5500 Reynolds number shown a non-uniform variation of temperature across length of the duct. The highest temperature is 325K and the lowest is 300K. The maximum temperature is seen near the rib end position.

The pressure at the inlet is higher and reduces as it moves towards the exit as shown in Figure 18. The pressure is higher in between the ribs facing towards the inlet face as shown by the red color.

18.png

Figure 18. Pressure plot at 3900 Reynolds number

The velocity plot shown in Figure 19 below shows a reduction in velocity between ribs and near to rib row shown by light blue and dark blue color. The maximum velocity attained is near the outlet section shown by dark red color. The velocity difference between the absorber face and rib face at the bottom causes’ vortex generation. The vortex or turbulent flow increases the heat transfer rate. The maximum velocity attained is 2.45 m/s and the minimum velocity attained is .012 m/s. The difference between maximum and minimum velocity is higher across the length of the duct thereby creating a higher pressure drop. Table 5 shows that the Nusselt number increases with an increase in the Reynolds number for all angles of ribs.

19.png

Figure 19. Velocity plot at 3900 Reynolds number

Table 5. Nusselt number of different angle ribs

Figure 20 shows that Nusselt number increases with increase in Reynolds number for all angles of ribs.

20.png

Figure 20. Nusselt number VS. Reynolds number

At low Reynolds number i.e. 3900 and 5500, 120° rib angle and 90° rib angle has almost same value and for higher Reynolds number 90° rib angle exhibited higher Nusselt number.

At low Reynolds numbers i.e. 3900 and 5500, 120° rib angle and 90° rib angle have almost the same value, and for higher Reynolds numbers 90° rib angle exhibited a higher Nusselt number. The friction factor is calculated using the pressure difference obtained from the CFD solution and tabulated in Table 6.

Table 6. Friction factor at different rib angles

Friction factor generally decreases with increase in Reynolds number as can be seen in Figure 21. At 60° rib angle friction factor first increases then decreases with increase in Reynolds number. At 120° rib angle friction factor decreases after 8500 Reynolds number.

21.png

Figure 21. Friction factor VS. Reynolds number

The friction factor generally decreases with an increase in Reynolds numbers. At a 60° rib angle friction factor first increases and then decreases with an increase in Reynolds number. At a 120° rib angle friction factor decreases after 8500 Reynolds number. THPF is calculated using the ratio of Nusselt number and friction factor which is tabulated in Table 7.

Table 7. THPF at different rib angles

The THPF value is found to be highest for 600 rib angles with the maximum value of 1.47 at 15500 Reynolds number. A minimum THPF value is observed for 900 rib angles at 3900 Reynolds number with a value of 1.033. In the aspect of higher Reynolds numbers, 1200 rib angles have consistently ensured the lowest THPF compared to the other two rib angles. THPF VS. Reynolds number is shown in Figure 22.

As its evident from Figure 22 THPF value is found to be highest for 600 rib angles with maximum value of 1.47 at 15500 Reynolds number. Minimum THPF value is observed for 900 rib angles at 3900 Reynolds number with value of 1.033. For higher Reynolds number 1200 rib angles has shown lowest THPF values compared to other two rib angles.

22.png

Figure 22. THPF VS. Reynolds number