© 2025 The authors. This article is published by IIETA and is licensed under the CC BY 4.0 license (http://creativecommons.org/licenses/by/4.0/).
OPEN ACCESS
In recent years, the integration of swarm intelligence-based metaheuristic optimization techniques into Artificial Intelligence (AI) has garnered significant attention. This project aims to investigate the potential applications of swarm intelligence techniques within the domain of AI. By leveraging the collective behavior and adaptive nature of swarm intelligence, these metaheuristic optimization methods offer unique opportunities for solving complex problems in AI. Numerous optimization methods have been proposed in academic research to address clustering-related challenges, but swarm intelligence has established a prominent position in the field. Particle swarm optimization (PSO) is the most popular swarm intelligence technique and one of the researchers' favorite areas. In this study, we introduce a novel clustering approach that integrates PSO with the K-means algorithm, aimed at enhancing clustering outcomes by effectively addressing common clustering challenges. The PSO algorithm has been shown to converge successfully during the initial stages of a global search, but around the global optimum. The proposed algorithm is designed to organize a given dataset into multiple clusters. To assess its effectiveness, we tested the algorithm on five different datasets. We then compared its clustering performance with that of the K-means and PSO algorithms, evaluating it based on metrics such as execution time, accuracy, quantization error, and both intra-cluster and inter-cluster distances.
Artificial Intelligence (AI), optimization, machine learning, deep learning, distribution, swarm intelligence, metaheuristic
Significant advancements in Artificial Intelligence (AI) have greatly enhanced machines' ability to handle complex tasks and make intelligent decisions. However, traditional optimization methods [1] often face limitations when dealing with the complexity and non-linearity of real-world problems. To address these challenges, metaheuristic techniques, particularly those based on swarm intelligence, have emerged as a promising solution.
Swarm intelligence algorithms [2] draw inspiration from collective behaviors observed in natural systems, leveraging principles such as self-organization, adaptation, and cooperation to tackle complex optimization problems in AI. Their approach offers several advantages, including robustness, flexibility, parallelism, and the ability to explore vast solution spaces, leading to near-optimal solutions in various AI domains.
Despite these advantages, the use of metaheuristics poses challenges. They often require meticulous parameter tuning [3], and their performance can be influenced by problem representation and search space characteristics. Additionally, the computational complexity associated with swarm intelligence algorithms may limit their use in resource-constrained environments.
This study aims to investigate the application of metaheuristic optimization methods, particularly those based on swarm intelligence [4], in AI. Integrating these methods into AI can enhance the precision, efficiency, and robustness of existing algorithms for solving complex optimization problems of large dimensions.
The results provide valuable insights into the benefits and challenges involved in utilizing metaheuristic optimization methods in AI [5]. Several domains and applications [6] have shown promising results, including optimization of machine learning model parameters, feature selection, portfolio optimization, image recognition, and data clustering. Looking ahead, hybrid approaches combining metaheuristic optimization methods with other AI techniques pave the way for addressing even more complex and challenging optimization problems.
The proposal outlined in this document integrates K-means with PSO techniques to optimize the clustering process [7], improving both its effectiveness and accuracy. While K-means is widely used for partitioning data sets into distinct clusters, finding optimal cluster centroids can be challenging, especially with large-scale or high-dimensional data sets. Optimizing K-means clustering results using PSO aims to refine cluster centroids, thereby improving clustering precision and convergence speed. The effectiveness of this method is assessed using metrics like inter-cluster distance, intra-cluster distance, and quantification error.
The organization of this study is as outlined: In section 2, including a detailed examination of the PSO method. Section 3 explores the K-means clustering algorithm, delves into data clustering with PSO, and outlines and evaluates the suggested methodology. Section 4 details the experimental framework used to assess the proposed approach and provides a comparative analysis of the results. The final section, Section 5, synthesizes the results and offers a comprehensive summary of the research outcomes.
In the domain of optimization, metaheuristic methods have firmly established themselves as potent techniques for addressing intricate problems [8] that present substantial challenges, often being difficult or even infeasible to solve through traditional approaches. Metaheuristics provide flexible and efficient problem-solving strategies that can tackle a wide range of optimization challenges [9]. Metaheuristic methods leverage a range of natural phenomena, such as the behavior of ants, birds, or genetic evolution, and emulate these processes to facilitate the search for optimal solutions. Unlike exact optimization algorithms that guarantee finding the global optimum, metaheuristics offer approximate solutions with good quality within a reasonable computational time. The term metaheuristic reflects the higher-level nature of these methods. They are not problem-specific algorithms but serve as general frameworks that can be applied to various problem domains. Metaheuristics [10] provide a way to navigate the vast search space by intelligently exploring and exploiting different regions.
Swarm intelligence, a specific subset of metaheuristic methods [11], takes cues from the collective behaviors of social insects like ants, bees, or birds. These methods mimic the interactions and collaboration observed among individuals within a population to seek out optimal solutions. Metaheuristic techniques serve as notable examples of methods rooted in swarm intelligence. The strength of metaheuristic methods resides in their capacity to address intricate optimization challenges, encompassing scenarios marked by non-linearities, multiple objectives, or solution spaces with high dimensions. By leveraging the principles of exploration and exploitation, metaheuristics can efficiently navigate through the search space, adapt to changing conditions, and escape local optima. Hybrid approaches combining metaheuristic optimization methods [12] with other AI techniques open the way to solving even more complex and challenging optimization problems.
In this study, we present an innovative clustering method that fuses K-means [13] with PSO to improve the overall clustering performance. This hybrid method aims to improve the quality of clustering outcomes by leveraging the strengths of both techniques. Although the K-means algorithm is extensively utilized to divide datasets into distinct clusters, finding optimal cluster centroids can be difficult, especially for large-scale or high-dimensional datasets.
Optimizing K-means clustering results using PSO aims to refine cluster centroids, thereby improving clustering accuracy and convergence speed.
PSO overcomes the limitations inherent to conventional K-means methods, notably sensitivity to initial centroid placement and susceptibility to local optima. It endows the algorithm with global search capabilities, enabling it to explore various cluster configurations and gradually converge on better clustering results.
2.1 Particle swarm method
The PSO method was initially conceptualized and created by James Kennedy and Russell Eberhart [14, 15]. The algorithm is grounded in a simplified model that simulates social interactions between "agents" and collaboration between individuals [16]. These individuals can be, for example, birds or bees or bees called particles, and they use their individual experiences as well as the experience of the whole population to move around a given space (search domain) to find food. Thanks to the notion of collaboration, a particle that is a promising solution can attract the rest of the population to share in its benefits from its discovery. The PSO algorithm starts with the initialization of the particle population. the particles and velocities are randomly distributed. Each particle is assigned a velocity vector which is calculated according to each particle’s experience and the group’s motion. Particle positions are updated by the notion of velocity in each iteration. This iterative procedure continues until convergence is attained.
2.1.1 Definition of the method
In PSO, the social behaviour is represented by a mathematical equation that directs particles in their movement process [17]. A particle's movement is guided by three primary components: Inertia, cognition, and social interaction. Each of these components contributes to the overall equation:
1) The inertia component: This component directs the particle to continue moving in its current direction.
2) The cognitive element: The particle modifies its trajectory by moving toward the optimal solution it has identified during its exploration.
3) The social element: The particle's movement is guided by the optimal solutions discovered by neighboring particles within the collective swarm.
2.1.2 Formalization
In a d-dimensional space, a swarm particle i at time t can be represented by the following parameters:
- X: the particle's current position within the search space;
- V: Its velocity, indicating the direction and magnitude of movement;
- Pb: The position corresponding to the particle's personal best solution;
- Pg: The position representing the best-known solution across the entire swarm;
- f (Pb): The fitness evaluation of the particle's best-known solution;
- f (Pg): The fitness value of the best solution known to the whole swarm.
The displacement of particle i between iterations t and t+1 occurs according to the two Eq. (1) and Eq. (2):
$\begin{aligned} & \mathrm{v}_{i D(t+1)}=\mathrm{v}_{i D(t)}+\mathrm{C}_1 \mathrm{r}_1 \left(\mathrm{~Pb}_{i D(t)}-\mathrm{X}_{i D(t)}\right)+\mathrm{C}_2 \mathrm{r}_2\left(\mathrm{Pg}_{i D(t)}-\mathrm{X}_{i D(t)}\right)\end{aligned}$ (1)
$\mathrm{X}_{i D(t+1)}=\mathrm{X}_{i D(t)}+\mathrm{V}_{i D(t)}$ (2)
C1, C2: Acceleration coefficients that control the influence of cognitive and social components on the particle's velocity.
r1, r2: Stochastic factors, represented by random numbers uniformly drawn from the interval [0, 1], which introduce randomness into the search process.
2.1.3 Algorithm steps
PSO is a metaheuristic inspired by the collective behavior observed in bird flocks [18]. It aims to replicate how these groups coordinate their movements and collectively optimize their paths. This bio-inspired technique has been successfully applied across various domains [19], particularly for solving optimization problems by mimicking natural system dynamics. The PSO algorithm simulates the coordinated motion of particles within a multidimensional search space to identify optimal solutions.
The fundamental PSO algorithm, as introduced by the study [14], begins by randomly initializing particles within the search space, assigning each particle an initial position and velocity [17]. During each iteration, particles update their positions and velocities according to Eq. (1) and Eq. (2), and their fitness values are evaluated. This process allows the determination of the best global position Pg. Both the personal best positions Pb, and the global best position Pg are updated iteratively following the procedure illustrated in Figure 1.
Figure 1. Particle swarm optimization (PSO) steps
The process [20] is repeated until the stopping criterion is satisfied.
1. Initialization:
- Set the population size, typically represented by a group of particles.
- Randomly set particle positions and velocities across the search space. within the specified search space.
- Define an objective function to evaluate the quality of each particle's current position within the search space.
This function plays a pivotal role in assessing how effectively a particle's position aligns with the specified objectives.
2. Evaluation:
- Assess each particle's performance by evaluating the objective function relative to its current position in the search space.
3. Update Personal Best:
- Compare the current performance [21] metric of each particle with its previously recorded personal best value.
- If the current performance metric surpasses the previously recorded personal best, update the personal best value accordingly, and adjust the personal best position accordingly. This process ensures that each particle’s performance is continuously assessed and improved upon [22].
4. Update Global Best:
- Assess the fitness values of the optimal personal positions across the entire swarm.
- Locate the particle in the entire population with the highest fitness value.
- Refine the global best position by incorporating the personal best position of the particle that exhibits the highest fitness.
5. Updating Velocity and Position:
- Modify the velocity of each particle [23] based on its current velocity, personal best position, and the global best position.
- The updated velocity is computed by integrating cognitive and social components to effectively balance the search between exploring new regions and exploiting known areas of the search space.
- Update the position [24] of each particle by incorporating the new velocity into its current position.
6. Termination Condition:
- Establish a termination criterion [25], which may involve reaching a predefined maximum number of iterations or achieving a satisfactory solution.
- If the stopping criteria are not satisfied, repeat from step 2; otherwise, advance to the subsequent step.
7. Output:
- Present the global best position, which signifies the optimal solution attained by the algorithm.
8. Optional: Post-processing and Fine-tuning:
- Following the acquisition of the optimal solution, optional postprocessing techniques can be applied to refine and enhance the solution if necessary.
- Parameter Fine-Tuning: Modifying parameters such as population size, maximum velocity, or acceleration coefficients can enhance the algorithm's effectiveness for specific problem instances.
The iterative characteristic of PSO permits particles to navigate the search space under the influence of their individual experiences and the collective wisdom of the swarm. By continuously updating their velocities and positions, particles converge towards promising regions, eventually finding near-optimal or optimal solutions.
The K-means clustering algorithm is a widely recognized unsupervised learning method designed to segment a dataset into K-distinct clusters [26]. The primary goal is to minimize the total sum of squared deviations between data points and their corresponding cluster centroids [27]. Nonetheless, determining the most appropriate cluster centroids can pose a significant challenge, especially when working with high-dimensional or extensive datasets.
An effective strategy to improve the efficiency of the K-means algorithm entails improving its clustering results by applying PSO. PSO can be harnessed to fine-tune the positions of cluster centroids, leading to enhanced clustering accuracy and faster convergence. The core idea involves treating each particle as a potential set of K-cluster centroids and using the PSO algorithm to iteratively optimize their positions.
During the optimization process, each particle’s position signifies a unique set of K-centroids, with the objective function mathematically expressed as the summation of squared distances between data points and their nearest centroids. The PSO algorithm then endeavours to identify the optimal set of centroids that minimizes this objective function.
In each iteration, particles refine their positions based on their individually best-known positions (pbest) and the best-known positions among all particles (gbest). Particle movement is influenced by both their prior positions and the global best position discovered thus far. Through this iterative process, particles systematically explore the solution space to identify the optimal cluster centroids [28].
By amalgamating PSO with the K-means algorithm, the optimization process becomes more robust and adept at discovering superior clustering solutions. PSO aids in surmounting the limitations associated with the traditional K-means algorithm, including sensitivity to initial centroid placement and susceptibility to local optima. It furnishes the algorithm with global search capabilities, enabling it to explore diverse cluster configurations and progressively converge towards improved clustering results.
Optimizing K-means clustering [29] via PSO presents a promising avenue for enhancing the efficacy of this widely applied clustering methodology. It streamlines the automatic and efficient determination of optimal cluster centroids, ultimately resulting in improved clustering performance and more effective data representation across various applications.
3.1 K-means algorithm
The K-means [30] clustering method is a well-known unsupervised learning [31] approach utilized to group data points into K-distinct clusters. Its primary goal is to segregate data in a manner where points within the same cluster exhibit similarity, while those in separate clusters display dissimilarity. This algorithm finds application [32] in various domains.
The algorithm follows a sequence of key steps. In the first step, K-cluster centroids are initialized by randomly selecting K-data points from the dataset. These centroids act as the initial representatives for the clusters.
In the assignment phase, each data point is allocated to the cluster that has the nearest centroid. This process is determined by a distance metric such as Euclidean distance, which ensures that each point is accurately associated with the cluster that best represents its proximity to the centroid.
Following the assignment phase, the algorithm proceeds to the update step. In this stage, the centroids of each cluster are recalculated by computing. In this stage, the centroids of each cluster are recalculated by determining the mean of all data points allocated to that specific cluster. This recalibration reflects the new positions of the centroids based on the reallocated data points.
The algorithm continues to iterate between the assignment and update steps until it satisfies a predefined stopping criterion. Typically, convergence serves as the primary criterion, gauged by monitoring the shift in centroids between iterations. If the centroids’ positions stabilize, and the change falls below a predefined threshold, the algorithm concludes.
Upon convergence, the final cluster assignments and centroids define the clustering solution. Each data point is allocated to a specific cluster, while the centroids indicate the representative positions for each cluster.
It’s noteworthy that the K-means algorithm can be influenced by the initial placement of centroids. To mitigate this influence, it’s a common practice to execute the algorithm multiple times with different initializations and select the solution with the minimum sum of squared distances as the ultimate clustering result.
Despite its computational efficiency and widespread use, the K-means algorithm does possess certain limitations [33]. It assumes that clusters are spherical and have uniform variances. an assumption that may not always hold in real-world scenarios. Additionally, identifying the most suitable number of clusters (K) can be a challenging task. Furthermore, identifying the ideal number of clusters (K) can pose a challenging task, often necessitating domain expertise or supplementary techniques.
In summary, the K-means algorithm serves as a robust tool for categorizing data into distinct groups. As illustrated in Figure 2, the algorithm iteratively assigns data points to clusters based on their proximity to centroids, which are updated until convergence. By comprehending its steps and limitations, researchers and practitioners can effectively employ this algorithm to extract meaningful insights and patterns from their data.
Figure 2. K-means clustering algorithm
3.2 Adapting the PSO metaheuristic for K-means clustering
The adaptation of the PSO metaheuristic to the K-means clustering algorithm revolves around leveraging PSO to optimize the positions of cluster centroids [34]. The main goal is to discover the ideal cluster centroids that minimize the sum of squares within clusters, thereby enhancing clustering outcomes.
The adaptation process typically encompasses the subsequent stages:
1. Initialization: Commence by setting up a population of particles, with each particle representing a possible solution and corresponding to a set of K centroid positions for the clusters. The particle's position is encoded as a vector containing these centroid positions.
2. Fitness Evaluation: The fitness function assesses the quality of the clustering solution linked to each particle's centroid positions. K-means that the fitness function frequently quantifies the within-cluster sum of squares, gauging the quantification pertains to the collective squared distances between data points and their linked cluster centroids.
3. Velocity Update: Particle velocities are modified using their prior velocities, their individual best-known positions (pbest), and the global best. This adjustment steers the particle toward regions within the search space with the potential for enhancing clustering solutions.
4. Position Update: The position of each particle is modified according to its current velocity. This update affects the positions of centroid coordinates for each cluster.
5. Fitness Comparison: Following the position updates, the fitness function is reevaluated for each particle to ascertain its clustering quality. Adjustments are applied to the most optimal positions (pbest and gbest) by the fitness values.
6. Termination Criteria: The algorithm persists in velocity and position updates until it fulfils a predefined termination condition. This condition could involve reaching a predefined maximum number of iterations, attaining a specific fitness threshold, or meeting other convergence criteria.
Through the iterative updating of particle positions and velocities, PSO systematically traverses the search space to discover the optimal centroid positions to minimize the within-cluster sum of squares.
The incorporation of PSO into K-means clustering offers several advantages, including improved convergence speed, the capability to escape local optima, and robustness in handling intricate datasets with non-linear cluster boundaries. It stands as a potent optimization technique for attaining superior clustering solutions.
In conclusion, adapting PSO for K-means clustering represents a promising avenue to augment the algorithm’s performance and elevate the quality of the resultant clusters.
3.3 Optimizing data clustering: Synergies between K-means and PSO for enhanced performance
The combined use of K-means and PSO leverages the complementary strengths of these two algorithms to enhance clustering outcomes. K-means is known for its efficiency in quickly finding local solutions by minimizing intra-cluster distances, but it often suffers from sensitivity to the initial selection of centroids and may converge to local optima. In contrast, PSO excels at global search by maintaining a population of potential solutions (particles) and guiding them toward better solutions based on both individual and collective experience.
By integrating these methods, we capitalize on their respective strengths. PSO can direct the global search toward promising regions of the solution space, while K-means can locally refine these solutions to converge swiftly to high-quality local optima. This hybrid approach overcomes the individual limitations of each algorithm, leading to more efficient convergence and higher-quality solutions.
Theoretically, the synergy between these algorithms can be explained by their foundational principles. PSO is inspired by the collective behavior of birds flocking or fish schooling, where particles explore the search space in pursuit of optimal solutions. K-means, on the other hand, iteratively updates centroids to minimize distances between data points and their respective centroids.
By combining these approaches, the system benefits from PSO's ability to explore the search space thoroughly, while K-means focuses on fine-tuning solutions in promising regions. This results in a more comprehensive exploration of the solution space and quicker convergence to high-quality solutions, ultimately enhancing performance compared to the use of either algorithm individually.
3.4 Proposed approach
The proposed method incorporates a hybridization approach that merges two algorithms: PSO and K-means. PSO is renowned for its effectiveness in global search but exhibits limitations in local search, especially when handling extensive or complex datasets. Conversely, K-means excels in local search but struggles with global clusters and can produce inconsistent results due to variations in initial partitions.
The principal goal of this research is to mitigate these limitations by synergizing the strengths of both algorithms. The proposed hybridization technique operates sequentially, involving the following steps:
a. The iteration process reaches the predefined maximum number of cycles.
b. The average shift in centroid vectors becomes smaller than a specified threshold value.
The integration of the PSO and K-means algorithms in this hybrid approach surpasses the individual use of either algorithm.
The PSO algorithm operates as a stochastic technique for discovering optimal solutions. To determine the termination criteria for PSO, it is recommended to run the algorithm multiple times. Each run generates a new optimal solution in the vicinity of the global optimum. These runs provide a robust foundation for further processing with K-means, ultimately leading to enhanced results.
In the initial stage [35], PSO is utilized to perform a global search and identify an initial solution close to the global optimum. The result obtained from PSO serves as the starting point for the K-means data clustering algorithm, which refines the solution and produces the final optimal result. This hybrid approach capitalizes on the complementary strengths of PSO and K-means to achieve superior clustering outcomes.
To evaluate the efficiency of the presented approach, we conducted a comparative analysis with each algorithm, PSO, and K-means. This analysis aims to assess how the presented technique performs in comparison to using each algorithm separately.
By drawing comparisons between the results achieved through our proposed approach and those attained by utilizing PSO and K-means independently, our objective is to achieve a profound understanding of the effectiveness and efficiency of our approach through this comparative analysis. This in-depth assessment serves as a pivotal step in gauging the feasibility and potential advantages of the hybridization technique we propose.
To facilitate this evaluation, we can employ various evaluation metrics and measures, including but not limited to clustering accuracy, convergence speed, computation time, and result stability. A meticulous analysis of these metrics enables researchers to gauge the extent to which our proposed approach excels in terms of clustering performance and other pertinent criteria when contrasted with the individual algorithms.
The comparative analysis conducted in this section not only shines a light on the strengths and limitations of the individual algorithms but also offers a deeper understanding of the benefits brought forth by our hybrid approach. Ultimately, this analysis significantly contributes to the comprehensive evaluation and assessment of the proposed hybridization technique.
The structure of this paper can be summarized as follows:
Section 4.1, we furnish a detailed depiction of the test dataset, shedding light on its characteristics and properties. This section lays the groundwork for subsequent evaluations and analyses.
Section 4.2 is dedicated to the presentation of various quality assessment parameters. These parameters play a pivotal role in quantitatively evaluating the clustering results, facilitating a thorough analysis of the method’s quality and accuracy.
In Section 4.3, we present the findings and outcomes stemming from the experiments conducted with the proposed method. We delve into the results, offering insights into the performance, efficiency, and effectiveness of our approach in comparison to the individual algorithms.
By presenting the article in this style, our objective is to offer readers a well-organized and logically structured presentation of the test dataset. Quality assessment parameters, and experimental findings. This structured approach facilitates a methodical understanding and evaluation of the performance of the proposed technique.
4.1 Test datasets
4.1.1 Iris dataset
The Iris dataset stands as a cornerstone in the realm of pattern recognition. It comprises 150 instances, meticulously categorized into three distinct classes, each corresponding to a particular variety of iris plants. The dataset encompasses four attributes, offers insights into three classes, and presents a total of 150 data vectors.
4.1.2 Wine problem
This dataset stems from a chemical analysis of wines produced in a specific Italian region, though sourced from three different grape varieties. The analysis accurately quantified the concentrations of 13 distinct chemical compounds across the three wine types. The dataset comprises 13 attributes, representing three classes, and contains a total of 178 data samples.
4.1.3 Artificial problem (Random Function)
For our study, we've generated an artificial dataset using the rand function in MATLAB. This dataset features four attributes and a collection of 100 data vectors.
4.1.4 Artificial problem I
The formulation of this problem respects the classification rule stated by Engelbrecht [18] as follows:
$\text{class} =\left\{\begin{array}{cc}1 & \text { if }\left(z_1 \geq 0.7\right) \text { or }\left(\left(z_1 \leq 0.3\right)\right. \left.\text { and }\left(z_2 \geq-0.2-z_1\right)\right) \\ 0 & \text { otherwise }\end{array}\right.$ (3)
A total of 400 data vectors were randomly created, with $z_1, z_2 \sim U(-1,1)$.
4.1.5 Artificial problem II
This problem is a 2-dimensional problem featuring four distinct classes. An intriguing aspect of this problem is that just one of the input dimensions significantly influences class formation.
A total of 600 patterns were drawn from four independent bivariate normal distributions, where classes were distributed according to for $i=1, \cdots, 4$, where p is the mean vector and $\mu$ is the covariance matrix; $m_1=-3, m_2=0, m_3=3$, and $m_4=6$.
$N_2\left(\mu=\binom{m_i}{0}, \sum=\left[\begin{array}{ll}0.50 & 0.05 \\ 0.05 & 0.50\end{array}\right]\right)$ (4)
4.2 Basic criteria
4.2.1 Quantization error
The primary objective focuses on minimizing the average squared quantization error, which quantifies the discrepancy between a data point and its corresponding representation. The mathematical formulation of this quantization error is as follows:
$Q_e=\sum_{j=1}^K\left[\sum_{i=1}^{N_j}\left\|x_i^j-c_j\right\|^2 / N_j\right] / K$ (5)
Lower quantization errors indicate superior data clustering.
4.2.2 Execution time
Execution time refers to the total time spent on the data clustering process. Minimizing execution time is desirable.
4.2.3 Intercluster distance
The intercluster distance is the separation between the centroids of clusters [19], as described in the Eq. (6):
$\operatorname{Inter} =\left(\left\|c_i-c_j\right\|\right)^2$ (6)
where, $c_i$ and $c_j$ represent the centroids of clusters i and j, respectively.
Larger intercluster distances indicate more effective data clustering, as they signify greater separation between clusters.
4.2.4 Intra-cluster distance
The intra-cluster distance, also known as the distance between particles and centroids within a cluster, is a key measure. It can be better understood by Utilizing the formula provided in the subsequent Eq. (7).
$\operatorname{Intra}=\frac{1}{n} \sum_{j=1}^k\left\|x_i^j-c_j\right\|^2$ (7)
where,
• C is the number of clusters.
• $c_j$ is the centroid of cluster j.
• N is the number of particles.
• $\left\|x_i^j-c_j\right\|$ is the distance between particles and the centroid of their respective clusters. Smaller intra-cluster distances indicate more cohesive and better-defined data clusters.
4.2.5 Accuracy
Clustering operates under the premise that two documents are allocated to the same cluster exclusively when they demonstrate similarity. Accuracy serves as the metric for quantifying the percentage of accurate decisions. and is often referred to as the Rand Index. It can be understood using the formula presented in the following Eq. (8):
$\operatorname{Accuracy}=(T P+T N) /(T P+F P+F N+T N)$ (8)
• TP: This refers to making accurate decisions where two similar documents are properly allocated to the same cluster.
• TN: This entails true negative decisions, which involve correctly assigning two dissimilar documents to different clusters.
• FP: This signifies incorrect decisions where two dissimilar documents are wrongly assigned to the same cluster.
• FN indicates false negative decisions, where two similar documents are erroneously assigned to different clusters.
Higher accuracy indicates better data clustering, as it reflects a greater number of correct decisions regarding document similarities and cluster assignments.
4.3 Experimental results
In our performance evaluation, we take into account four key criteria: Execution time, quantization error, intra-cluster distance, and inter-cluster distance.
4.3.1 Evaluation based on execution time
Execution time, which refers to the total time required for the data clustering process, is a crucial performance metric.
Table 1 provides a summary of the algorithm comparison in terms of execution time.
Table 1. Performance evaluation based on execution time
|
Algorithms |
Iris |
Wine |
Artificial Dataset |
Artificial Problem I (400) |
Artificial Problem II (600) |
|
K-means |
3.13 |
3.73 |
2.94 |
4.12 |
5.08 |
|
PSO |
4.63 |
5.19 |
3.96 |
5.64 |
6.82 |
|
Hybrid |
7.34 |
8.76 |
5.62 |
8.45 |
10.11 |
An algorithm is generally considered more efficient when it requires less execution time. In this context, Figure 3 presents a line chart that illustrates the execution times of the K-means, PSO, and hybrid clustering algorithms across several benchmark datasets. This visual representation provides an intuitive understanding of each algorithm's computational cost. Furthermore, Figure 4 offers a comparative analysis using a bar chart, allowing for a clearer interpretation of execution time differences across datasets and facilitating the evaluation of each method's computational efficiency.
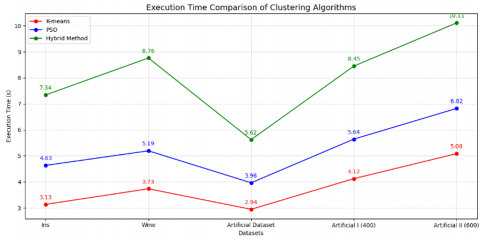
Figure 3. Line chart comparing inter execution time
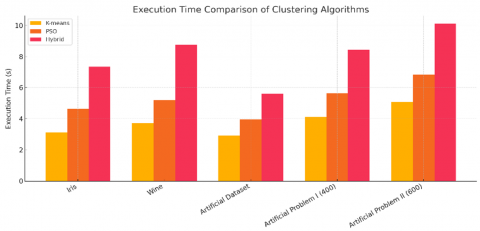
Figure 4. Across benchmark datasets execution time comparison of clustering algorithms
4.3.2 Evaluation based on quantization error
The quantization error plays a crucial role in evaluating the performance of these algorithms. Table 2 offers a concise overview of the comparison among these algorithms concerning Quantization Error.
Table 2. Performance evaluation based on quantization error
|
Algorithms |
Iris |
Wine |
Artificial Dataset |
Artificial Problem I (400) |
Artificial Problem II (600) |
|
K-means |
0.6521 |
1.5901 |
2.2266 |
0.9840 |
0.2640 |
|
PSO |
0.5782 |
1.4199 |
1.8758 |
0.7690 |
0.2520 |
|
Hybrid |
0.4873 |
1.1167 |
1.6364 |
0.7680 |
0.2500 |
Minimizing quantization error remains a fundamental objective in clustering, as it indicates the effectiveness of an algorithm in capturing the intrinsic structure of the data. Figure 5 presents a line chart illustrating the quantization error values obtained by K-means, PSO, and the proposed Hybrid approach across five benchmark datasets. This graphical representation enhances the interpretability of the comparative performance. In parallel, Figure 6 provides a bar chart that reinforces the observation that the Hybrid method consistently yields the lowest quantization error values.
Figure 5. Line chart comparing quantization error
Figure 6. Quantization error comparison of clustering algorithms across benchmark datasets
The results highlight the superiority of the Hybrid algorithm over the standalone techniques, confirming its enhanced capability to produce compact and representative clusters.
4.3.3 Evaluation based on intra cluster distance
Intra-cluster distance, denoting the proximity between particles and centroids within a cluster, is pivotal in assessing the quality of clustering [36]. The definition of intra-cluster distance can be found in the equation. Table 3 offers a comprehensive comparison of these algorithms concerning intra-cluster distance.
Table 3. Performance evaluation based on intra-cluster distance
|
Algorithms |
Iris |
Wine |
Artificial Dataset |
Artificial Problem I |
Artificial Problem II |
|
K-means |
1.6498 |
3.2015 |
2.3694 |
3.678 |
0.911 |
|
PSO |
1.94 |
3.0625 |
1.6169 |
3.826 |
0.873 |
|
Hybrid |
1.6205 |
2.7064 |
1.8381 |
3.823 |
0.869 |
In clustering evaluation, the intra-cluster distance is a key metric used to assess the compactness of clusters. A smaller intra-cluster distance indicates that data points within a cluster are closely grouped, which generally reflects higher clustering quality and internal consistency.
To assess and compare the performance of the K-means, PSO, and the proposed hybrid algorithm, experiments were conducted on five benchmark datasets: Iris, Wine, Artificial, Artificial I, and Artificial II. The results, in terms of intra-cluster distance, are visualized in Figure 7 and Figure 8 for clarity and intuitive understanding.
Figure 7. Line chart comparing intra-cluster distances
Figure 8. Bar chart comparing intra-cluster distances
As illustrated in Figure 7, the line chart reveals that the hybrid method consistently achieves lower intra-cluster distances across most datasets compared to the individual algorithms. This trend indicates that the hybrid approach is more effective in forming tightly packed clusters.
In addition, Figure 8 presents a bar chart offering a direct visual comparison of intra-cluster distances for all three algorithms across the datasets. This form of visualization emphasizes the superiority of the hybrid model, particularly in datasets where both K-means and PSO show higher intra-cluster variation.
These findings suggest that the hybrid algorithm benefits from the global search capabilities of PSO and the local refinement strength of K-means, resulting in more coherent clustering outcomes. The consistently lower intra-cluster distances validate the hybrid approach’s capacity to discover high-quality clustering structures.
4.3.4 Evaluation based on inter-cluster distance
The inter-cluster distance, which measures the separation between cluster centroids, is a fundamental metric for assessing clustering quality. This concept, further defined by an equation, is summarized comparatively for different algorithms in Table 4. Generally, higher inter-cluster distances indicate better clustering performance by reflecting clearer separation and stronger distinction between groups.
Table 4. Performance evaluation based on inter-cluster distance
|
Algorithms |
Iris |
Wine |
Artificial Dataset |
Artificial Problem I |
Artificial Problem II |
|
K-means |
1.6598 |
1.1863 |
1.4869 |
1.7710 |
0.7960 |
|
PSO |
1.4134 |
1.2476 |
1.3937 |
1.1420 |
0.8150 |
|
Hybrid |
1.7579 |
1.4346 |
1.5976 |
1.1510 |
0.8140 |
Inter-cluster distance serves as a critical measure of clustering quality, as it reflects how well-separated the resulting clusters are. A larger inter-cluster distance generally indicates a more effective clustering algorithm, as it suggests clearer boundaries and greater dissimilarity between groups.
To improve the interpretability of these results and enable a visual comparison between the algorithms, Figure 9 presents the inter-cluster distances using a line chart, showing performance trends across the five datasets. In parallel, Figure 10 provides a bar chart offering a more direct and dataset-specific comparison. Together, these visualizations illustrate the relative effectiveness of K-means, PSO, and the proposed hybrid approach in achieving meaningful separation between clusters.
Figure 9. Comparison of inter-cluster distances-line chart
Figure 10. Comparison of inter-cluster distances-bar chart
The method presented in this study demonstrates larger inter-cluster distances when compared to both individual algorithms, offering compelling evidence of its superiority.
4.3.5 Comparison based on accuracy
Accuracy, which signifies the ratio of correctly grouped data items into the most suitable clusters, serves as a crucial metric for evaluating the performance of clustering algorithms. Table 5 offers a comprehensive comparative analysis of these algorithms in terms of accuracy.
Table 5. Performance comparison based on accuracy
|
Algorithms |
Iris |
Wine |
Artificial Dataset |
Artificial Problem I |
Artificial Problem II |
|
K-means |
76.18% |
72.63% |
68.69% |
70.42% |
66.25% |
|
PSO |
81.27% |
82.12% |
78.32% |
83.10% |
79.87% |
|
Hybrid |
88.20% |
86.73% |
82.31% |
89.45% |
85.62% |
Accuracy, which signifies the ratio of correctly grouped data items into the most suitable clusters, serves as a crucial metric for evaluating the performance of clustering algorithms. Table 5 offers a comprehensive comparative analysis of these algorithms in terms of Accuracy.
Accuracy is a fundamental metric for evaluating clustering algorithms, where higher accuracy signifies a more effective approach in correctly assigning data points to their respective clusters. To visually illustrate and compare these accuracy scores, Figure 11 and Figure 12 offer a comprehensive overview: Figure 11 displays the results in a line chart, while Figure 12 presents the same data in a bar chart format, enabling clear and direct comparison of each algorithm’s performance.
Figure 11. Accuracy comparison (line chart)
Figure 12. Comparative accuracy of clustering algorithms on benchmark datasets
The presented method showcases superior accuracy when compared to both individual algorithms. This clear superiority underscores the advantage of the proposed approach. Achieving higher accuracy, it outperforms individual algorithms and offers a more reliable and accurate solution for the problem at hand. This finding strengthens the argument that the proposed approach is the preferred choice for achieving accurate and robust clustering results.
This project delved into the utilization of swarm intelligence meta-heuristic optimization techniques in the realm of AI through an exhaustive analysis of existing literature and practical experiments. Swarm intelligence algorithms [21] have demonstrated their utility in tackling complex optimization challenges within AI. These algorithms offer key advantages such as robustness, flexibility, parallelism, and global search capabilities, thus enhancing the accuracy, efficiency, and robustness of AI applications, spanning machine learning, data mining, pattern recognition, and optimization.
In this study, we investigated the application of metaheuristic optimization techniques based on swarm intelligence in the field of AI. Our primary objective was to assess the advantages of these algorithms across various AI applications, with a specific focus on data clustering.
We observed that integrating metaheuristic optimization, particularly by combining the K-means algorithm with PSO, holds promising prospects for enhancing the performance of clustering algorithms. By fine-tuning the centroids' positions using PSO, we managed to expedite the convergence of clustering algorithms while enhancing their precision, a critical aspect in effectively managing complex datasets.
Furthermore, our approach facilitated exhaustive exploration of the solution space, enabling us to pinpoint the optimal cluster centroids. This represents a significant advancement in the AI domain, where solution quality is paramount.
Additionally, we introduced a novel cooperative algorithm leveraging PSO and the K-means algorithm. Our hybrid approach amalgamates PSO's global search capability with K-means' rapid convergence, thus circumventing the limitations of both methods.
The outcomes of our experiments illustrated that our hybrid approach outperformed K-means and PSO algorithms individually. We observed improved convergence, lower quantization errors, larger inter-cluster distances, and smaller intra-cluster distances, all while maintaining a similar execution time.
In conclusion, our study reaffirmed the efficacy and relevance of the hybrid approach combining K-means and PSO in the realm of data clustering. By delivering promising results and opening up new research avenues, this study contributes to enriching the toolkit of AI researchers and fostering future advancements in the field of data clustering.
[1] Mandal, P.K. (2023). A review of classical methods and Nature-Inspired Algorithms (NIAs) for optimization problems. Results in Control and Optimization, 13: 100315. https://doi.org/10.1016/j.rico.2023.100315
[2] Bari, A., Zhao, R., Pothineni, J.S., Saravanan, D. (2023). Swarm intelligence algorithms and applications: An experimental survey. In International Conference on Swarm Intelligence, pp. 3-17. https://doi.org/10.1007/978-3-031-36622-2_1
[3] Joshi, S.K., Bansal, J.C. (2020). Parameter tuning for meta-heuristics. Knowledge-Based Systems, 189: 105094. https://doi.org/10.1016/j.knosys.2019.105094
[4] Dong, J. (2023). Recent Advances in Swarm Intelligence Algorithms and Their Applications. MDPI-Multidisciplinary Digital Publishing Institute.
[5] Kaur, A., Kumar, Y., Sidhu, J. (2024). Exploring meta-heuristics for partitional clustering: Methods, metrics, datasets, and challenges. Artificial Intelligence Review, 57(10): 287. https://doi.org/10.1007/s10462-024-10920-1
[6] Sunaina, S., Shivahare, B.D., Kumar, V., Gupta, S.K., Singh, P., Diwakar, M. (2023). Metaheuristic optimization algorithms and recent applications: A comprehensive survey. In 2023 International Conference on Computational Intelligence, Communication Technology and Networking (CICTN), Ghaziabad, India, pp. 506-511. https://doi.org/10.1109/CICTN57981.2023.10140511
[7] Chen, C.Y., Ye, F. (2012). Particle swarm optimization algorithm and its application to clustering analysis. In 2012 Proceedings of 17th Conference on Electrical Power Distribution, Tehran, Iran, pp. 789-794.
[8] Osaba, E., Villar-Rodriguez, E., Del Ser, J., Nebro, A. J., Molina, D., et al. (2021). A tutorial on the design, experimentation and application of metaheuristic algorithms to real-world optimization problems. Swarm and Evolutionary Computation, 64: 100888. https://doi.org/10.1016/j.swevo.2021.100888
[9] Banerjee, A., Singh, D., Sahana, S., Nath, I. (2022). Impacts of metaheuristic and swarm intelligence approach in optimization. In Cognitive Big Data Intelligence with a Metaheuristic Approach, pp. 71-99. https://doi.org/10.1016/B978-0-323-85117-6.00008-X
[10] Agarwal, S., Kumar, S. (2024). Survey on clustering problems using metaheuristic algorithms. In 2024 11th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, pp. 1-5. https://doi.org/10.1109/ICRITO61523.2024.10522107
[11] Wang, C., Zhang, S.Y., Ma, T.H., Xiao, Y.T., Chen, M.Z., Wang, L. (2025). Swarm intelligence: A survey of model classification and applications. Chinese Journal of Aeronautics, 38(3): 102982. https://doi.org/10.1016/j.cja.2024.03.019
[12] Raidl, G.R., Puchinger, J., Blum, C. (2018). Metaheuristic hybrids. In Handbook of metaheuristics, pp. 385-417. https://doi.org/10.1007/978-3-319-91086-4_12
[13] Oti, E.U., Olusola, M.O., Eze, F.C., Enogwe, S.U. (2021). Comprehensive review of K-means clustering algorithms. International Journal of Advances in Scientific Research and Engineering, 7(8): 64-69. https://doi.org/10.31695/ijasre.2021.34050
[14] Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. In Proceedings of ICNN'95-international conference on neural networks, 4: 1942-1948. https://doi.org/10.1109/ICNN.1995.488968
[15] Cuevas, E., Rosas Caro, J.C., Alejo Reyes, A., González Ayala, P., Rodriguez, A. (2025). The particle swarm optimization method. In Optimization in Industrial Engineering: From Classical Methods to Modern Metaheuristics with MATLAB Applications, pp. 159-172. https://doi.org/10.1007/978-3-031-74027-5_9
[16] Kennedy, J. (1997). The particle swarm: Social adaptation of knowledge. In Proceedings of 1997 IEEE International Conference on Evolutionary Computation (ICEC'97), Indianapolis, IN, USA, pp. 303-308. https://doi.org/10.1109/ICEC.1997.592326
[17] Shami, T.M., El-Saleh, A.A., Alswaitti, M., Al-Tashi, Q., Summakieh, M.A., Mirjalili, S. (2022). Particle swarm optimization: A comprehensive survey. IEEE Access, 10: 10031-10061. https://doi.org/10.1109/ACCESS.2022.3142859
[18] de Wet, R.M., Engelbrecht, A. (2023). Set-based particle swarm optimization for data clustering: Comparison and analysis of control parameters. In Proceedings of the 2023 7th International Conference on Intelligent Systems, Metaheuristics & Swarm Intelligence, pp. 103-110. https://doi.org/10.1145/3596947.3596956
[19] Gad, A.G. (2022). Particle swarm optimization algorithm and its applications: A systematic review. Archives of computational methods in engineering, 29(5): 2531-2561. https://doi.org/10.1007/S11831-021-09694-4
[20] Marini, F., Walczak, B. (2015). Particle swarm optimization (PSO). A tutorial. Chemometrics and Intelligent Laboratory Systems, 149: 153-165. https://doi.org/10.1016/j.chemolab.2015.08.020
[21] Guo, W.A., Si, C.Y., Xue, Y., Mao, Y.F., Wang, L., Wu, Q.D. (2017). A grouping particle swarm optimizer with personal-best-position guidance for large scale optimization. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 15(6): 1904-1915. https://doi.org/10.1109/TCBB.2017.2701367
[22] Sato, Y., Yamashita, Y., Guo, J. (2023). PSO with local search using personal best solution for environments with small number of particles. In International Conference on Swarm Intelligence, pp. 123-135. https://doi.org/10.1007/978-3-031-36622-2_10
[23] Wang, C.F., Song, W.X. (2019). A modified particle swarm optimization algorithm based on velocity updating mechanism. Ain Shams Engineering Journal, 10(4): 847-866. https://doi.org/10.1016/j.asej.2019.02.006
[24] Tijjani, S., Ab Wahab, M.N., Noor, M.H.M. (2024). An enhanced particle swarm optimization with position update for optimal feature selection. Expert Systems with Applications, 247: 123337. https://doi.org/10.1016/j.eswa.2024.123337
[25] Bassimir, B., Schmitt, M., Wanka, R. (2020). Self-adaptive potential-based stopping criteria for particle swarm optimization with forced moves. Swarm Intelligence, 14(4): 285-311. https://doi.org/10.1007/s11721-020-00185-z
[26] Oti, E.U., Olusola, M.O., Eze, F.C., Enogwe, S.U. (2021). Comprehensive review of K-means clustering algorithms. Criterion, 12: 22-23. http://doi.org/10.31695/IJASRE.2021.34050
[27] Sarang, P. (2023). Centroid-Based Clustering. Thinking Data Science, pp. 171-183. https://doi.org/10.1007/978-3-031-02363-7_9
[28] Mangat, V. (2012). Survey on particle swarm optimization based clustering analysis. In International Symposium on Evolutionary Computation, pp. 301-309. https://doi.org/10.1007/978-3-642-29353-5_35
[29] Xiao, E. (2024). Comprehensive K-means Clustering. Journal of Computer and Communications, 12(3): 146-159. https://doi.org/10.4236/jcc.2024.123009
[30] Suyal, M., Sharma, S. (2024). A Review on Analysis of K-means Clustering Machine Learning Algorithm based on Unsupervised Learning. Journal of Artificial Intelligence and Systems, 6: 8-95. https://doi.org/10.33969/AIS.2024060106
[31] Naeem, S., Ali, A., Anam, S., Ahmed, M.M. (2023). An unsupervised machine learning algorithms: Comprehensive review. International Journal of Computing and Digital Systems, 13(1). http:/doi.org/10.12785/ijcds/130172
[32] Singh, J., Singh, D. (2024). A comprehensive review of clustering techniques in Artificial Intelligence for knowledge discovery: Taxonomy, challenges, applications and future prospects. Advanced Engineering Informatics, 62: 102799. https://doi.org/10.1016/j.aei.2024.102799
[33] Karim, I., Daud, H., Zainuddin, N., Sokkalingam, R. (2024). Addressing limitations of the K-means clustering algorithm: Outliers, non-spherical data, and optimal cluster selection. AIMS Mathematics, 9(9): 25070-25097. http://doi.org/10.3934/math.20241222
[34] Gharehchopogh, F. S., Abdollahzadeh, B., Khodadadi, N., Mirjalili, S. (2023). Metaheuristics for clustering problems. In Comprehensive Metaheuristics, pp. 379-392. https://doi.org/10.1016/B978-0-323-91781-0.00020-X
[35] Sanprasert, P., Sodsri, C., Jewajinda, Y. (2022). Data clustering using particle swarm optimization for pairwise microarray bioinformatics data. In 2022 6th International Conference on Information Technology (InCIT), Nonthaburi, Thailand, pp. 120-124. https://doi.org/10.1109/InCIT56086.2022.10067388
[36] Binu Jose, A., Das, P. (2022). A multi-objective approach for inter-cluster and intra-cluster distance analysis for numeric data. In Soft Computing: Theories and Applications: Proceedings of SoCTA 2021, pp. 319-332. https://doi.org/10.1007/978-981-19-0707-4_30