© 2024 The authors. This article is published by IIETA and is licensed under the CC BY 4.0 license (http://creativecommons.org/licenses/by/4.0/).
OPEN ACCESS
The burgeoning demand for wireless networking and its associated applications has spurred academic endeavors to devise more efficient routing protocols. Wireless sensor networks (WSNs) operating on battery power, grapple with constraints such as quality of services (QoS) issues, energy dissipation, processing overhead, and link failures. Preserving the QoS is paramount for WSNs, as it directly impacts data transmission and overall network performance, rendering them unsuitable for real-time applications. So, this paper introduces a secure energy-efficient optimal routing framework. It is designed using Bayesian network and an Elicit Genetic Algorithm (EGA). The proposed model goal is to mitigate routing issues, enhance the QoS, and optimize energy efficiency. Path selection involves learning information about node/network connectivity and availability, enabling the derivation of disjoint paths without shared communication components. The simulation is done using the network simulator 2 tool to demonstrates the proposed routing protocol effectively facilitates communication by elevating quality of services, reducing energy consumption, and ensuring suitability for real-time applications. The evaluation of network communication effectiveness employs performance parameters such as end-to-end delay, throughput, energy dissipation, and packet loss, highlighting the robustness and efficiency of the proposed framework.
Bayesian network, ELICIT genetic algorithm, evolutionary computing, internet of things, wireless sensor network
The rapid expansion of wireless communication networks and associated applications has sparked a resurgence in research and industry efforts to develop more effective and resilient routing methods [1] to meet escalating demands. In the contemporary human existence, a communication system is indispensable, enabling users to share both known and undiscovered information, facilitating informed decision-making. However, there is a growing need for advancements in network computing and decision-making processes to enhance the quality of service in communication [2]. This involves ensuring timely, reliable, and energy-efficient communication among the network nodes. With the proliferation of internet of things (IoT) and machine-to-machine (M2M) communication, wireless communication protocols have become foundational for facilitating real-time data transfer across nodes to support efficient energy decision-making [3, 4]. These applications have expanded to encompass Big Data analytics, corporate communication, monitoring and control, and enhanced observational methods. Among the various proposed network models, wireless sensor networks (WSNs) have emerged as a prominent solution [5].
WSNs, known for their decentralized and infrastructure-less communication approach, consist of multiple sensor nodes distributed throughout the network. These nodes collaborate to relay detected data from source to sink nodes through one or more hops [6]. However, the dynamic natured network and the varying conditions of nodes often impact transmission efficiency, leading to challenges such as connection interruptions, congestion, packet loss, and the need for retransmissions. These issues result in increased energy consumption, thereby reducing the network's lifespan and compromising QoS standards. Both quality of service [7] and quality of experience (QoE) are critical aspects in traditional communication frameworks, necessitating WSNs to ensure optimal information transmission. Additionally, as WSNs operate on battery power, prudent routing decisions are essential to minimize packet loss, retransmission rates, and subsequent node failures, thereby maximizing network longevity.
In proposed research, we have developed a robust evolutionary computing (EC)-aided routing mechanism for dynamic network-aware routing decisions in WSNs. evolutionary computing, inspired by biological systems, encompasses a family of global optimization algorithms. Genetic algorithms, a type of EC [8] algorithm, that mimic biological evolution processes. These algorithms offer optimal solutions for global problems, making them suitable for optimizing routing in WSNs to minimize energy consumption. Within the realm of EC, including Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO), Agent-based modeling, distribution algorithms, multi-phase evolution, and artificial immune systems, are employed. Genetic algorithms, renowned for their ability to generate optimal solutions through the production of multiple individuals and the evaluation of fitness functions, are particularly noteworthy in this context.
The GA [9] initiates with a population of random chromosomes, each consisting of genes represented as binary digits. Through iterative processes involving mutation, crossover, and selection operators, the algorithm guides the population towards the optimal solution. There are variations such as steady-state GA and EGA, where one or two individuals from the population are replaced in each generation or every individual is replaced in every generation, respectively. Additionally, in the initialization phase, the communication radius between nodes, represented by the distance threshold, is set. Parent selection, a crucial step in the algorithm, involves identifying parents for producing offspring in the next generation through mating and recombination processes. Overall, this EC-based approach offers a promising solution for optimizing routing decisions in WSNs, thus enhancing energy efficiency and network performance.
The primary objective of this research is to enhance the longevity of energy-stressed networks by minimizing the power consumption of sensor nodes. In Wireless Sensor Networks (WSNs), the critical issue of energy scarcity necessitates innovative approaches to optimize the utilization of available resources. Various techniques, including topology management, smart routing, sleep cycle scheduling, and clustering, can be employed to mitigate power consumption within the network. Given the energy constraints in WSNs, where constant battery replenishment is challenging, this research concentrates on the development of energy-efficient routing technologies. The aim is to extend the operational life of WSNs by implementing strategies such as multi-sink repositioning, cluster-based reliable routing, and QoS-enhanced routing.
The proposed approach is designed to address such challenges based on the concept of disjoint paths with minimum or no-connected components. However, formulating such a routing model can pose a challenge as it falls into the realm of NP-hard problems. This entails dynamically learning node and network parameters and predicting a set of paths with minimal or no shared components. With this objective in mind, this paper presents a robust Optimal Routing Framework assisted by a Bayesian network and an EGA. The proposed EGA model adapts to the connectivity and availability of nodes as the objective function to derive the fully disjointed paths. EGA prioritizes low-connectivity loss and high availability of neighboring nodes to construct the Fully Disjointed Paths, while minimizing the number of hops and shared components. In the event of adversarial conditions like the presence of malicious nodes or node failure along a path, the model seamlessly switches to an alternate path, ensuring timely data transmission without requiring the retransmission of the entire dataset.
This work encompases the introduction of an advanced routing protocol, the incorporation of clustering and EGA techniques, the achievement of superior performance metrics, and the broad applicability of the protocol across diverse wireless sensor network domains. These contributions collectively advance the state-of-the-art in optimizing routing protocols.
1.1 Research contributions
The primary contributions of this study are outlined as follows:
1.2 Structure of the paper
The subsequent sections of the paper are outlined as follows: Section 2 delves into the existing body of work, followed by an exploration of research questions. Section 3 provides a detailed discussion of the identified issues, along with an overarching framework proposal and its implementation. The simulation outcomes and comparative results are presented in Section 4, while Section 5 wraps up the entire proposed work by offering concluding remarks on its outcomes. The references are listed in the final section of the paper.
Recent strides in wireless sensor networks have been significantly influenced by the integration of machine learning [10] techniques, especially in combating the energy depletion issue prevalent in these networks. A plethora of routing protocols and methodologies have emerged, highlighting the critical importance of bandwidth and power efficiency. Researchers have proposed and evaluated numerous ML-based mechanisms aimed at optimizing routing protocols to conserve power in these networks. The latest generation of sensor devices showcases heightened intelligence, efficiency, and longevity, boasting extended lifespans and diminished power consumption [11]. However, sensor nodes still grapple with power depletion stemming from suboptimal routing, presence of outliers in routing paths, or multiple shared nodes in forwarding paths. Several researches have designed various optimal routing schemes utilizing machine learning, data mining, and soft computing techniques.
For instance, in the study [12], cluster head selection hinges on traffic priority data and energy levels to establish the routes for data transmission. The study [13] introduces the energy efficient cluster-based routing algorithm, employing K-means clustering [3], optimal route selection, energy-based communication, and a mechanism for alternating between cluster heads [4] to enhance energy efficiency and network lifespan. Furthermore, the efficacy of EEDLABA is evaluated through a model for energy consumption and path loss, utilizing nine sensor nodes deployed on a human body [14]. The study [15] proposes a multicast routing protocol integrating reinforcement learning and modified transmission back-offs and acknowledgments, showcasing successful implementation of ML algorithms to resource-constrained devices.
Hu and Fei [10] resolve the issues related to propagation delay and power consumption in underwater wireless sensor nodes through a machine-learning approach. Hendriks, et al., [16] introduce the Q-learning-based energy-efficient and lifetime-aware routing protocol. This balanced routing protocol distributes routing responsibilities across all sensor nodes, leveraging hierarchical routing to optimize energy usage. Additionally, an energy-efficient shortest-path Q-routing algorithm based on reinforcement learning to prolong network lifetime.
The inherent dynamic topology of wireless sensor networks [17] adds complexity to the routing mechanism, posing a significant challenge. Another vital aspect is the need to minimize resource consumption during routing. To address these challenges, a support vector machine-based clustering method was introduced [18]. This method strategically allocates nodes to the closest cluster head to reduce energy consumption. A novel approach [19] proposes a Naive Bayesian-based classification method to predict traffic load and energy levels along selected paths. Estimating link costs among nodes is crucial for routing, and the study [20] suggest a machine learning-based approach to calculate these costs. To prolong network lifetime, Masoud et al. [21] introduce the hybrid clustering routing protocol-hole detection (HCRP-HD), focusing on hole and edge detection to reduce sensor node energy consumption. The sink node spearheads this detection, leading to the network's transformation into multiple rings designed to minimize energy consumption from direct transmission.
In recent research, a diverse array of ML techniques has been harnessed to solve the energy depletion challenge pervasive in wireless sensor networks. Notably, the latest generation of sensor devices boasts enhanced intelligence, efficiency, and longevity, yet they still grapple with energy depletion stemming from suboptimal routing and the presence of outliers in routing paths. Several studies have explored ML-driven routing schemes, aiming to optimize energy consumption and prolong network lifespan. For example, in the study [22], the user-specific optimal capacity shortest-path (US-OCSP) routing protocol utilizes machine learning to determine the shortest path considering node capacity and distance, effectively avoiding congested nodes using the Q-learning algorithm. Unlike traditional routing algorithms requiring high bandwidth, this method conducts on-demand route discovery and proactively updates routes to enhance throughput and bitrate. Additionally, Hendriks et al. [23] introduce a novel Q-learning-based algorithm that prioritizes packets in different traffic classes to address QoS concerns in reinforcement-learning-based algorithms. This algorithm routes packets via distinct routes, enhancing QoS parameters.
Another noteworthy approach is the Energy-Centric Route-Planning (ECRP) method proposed [24], which balances sensor node lifetime and routing security by considering individual and cooperative nodes' energy requirements. Furthermore, Yang et al. [25] combines reinforcement learning with Blockchain technology to propose an efficient and secure routing scheme. Here, Blockchain ensures the immutability of routing information, while reinforcement learning dynamically selects more trusted and efficient links. The integration of machine learning with routing protocols is a prevalent trend in recent research. For instance, Yao et al. [26] introduces a load-balanced routing protocol based on machine learning, utilizing Principal Component Analysis and neural networks to predict network queue status and make intelligent routing decisions. Similarly, Ghaffari [27] proposes a Q-learning-based method to mitigate end-to-end delay by predicting network node behavior patterns. Additionally, Strykhaliuk et al. [28] presents a genetic algorithm-based routing protocol that efficiently identifies unhealthy nodes, thus minimizes energy dissipation and computational time. Other approaches, such as the clustering-based routing protocol proposed [29], aim to extend network lifetime by segmenting the network as clusters with designated cluster heads for efficient data transport.
Furthermore, protocols like the Multi-Objective Multi-Hop Routing (MOMHR) protocol introduced [30] and the Chicken-Dragonfly (CHicDra) optimization algorithm proposed [31] focus on optimal routing and secure routing, respectively, utilizing machine learning techniques to enhance network performance and security. The literature also explores various challenges and concerns in energy-efficient routing, including data processing, node re-energization, QoS maintenance, scalability, protection, and intrusion detection. Outliers remain a significant challenge in WSNs, leading to abnormal behavior and security threats. However, recent advancements in ML-driven routing protocols offer promising solutions to these challenges, paving the way for more efficient and secure wireless sensor networks.
The proposed work is designed to mitigate significant constraints such as energy exhaustion and network lifetime issues. WSNs often face node death, leading to communication loss, data drop, and retransmissions, resulting in delays and energy depletion. To address these challenges and improve QoS and energy efficiency, research aims to establish a stable and effective EC-assisted WSN routing protocol. This proposed protocol incorporates Bayesian network with the FDDP model, supported by EC specifically, the Elitist Genetic Algorithm, which identifies dual-disjoint paths without shared segments to ensure QoS-centric and energy-efficient routing. The research objectives accomplished through this research include developing techniques for energy-efficient WSNs, ensuring low processing overhead for data transmission, and designing an optimal routing protocol using EC algorithms.
The overall proposed structures and their systematic implementation are primarily discussed in this section. As previously discussed, the primary goal of this study is to use dynamic node/network mining to make the best routing decisions possible. The EGA based FDDP aims to use different node parameters to allow a dual-disjoint path with less shared nodes/links for efficient and QoS communication. The proposed method employs a network mining concept to make dynamic routing decisions, it is vital to understand key network/node parameters.
3.1 EGA based FDDP
The proposed routing protocol detects malicious nodes and aims to prevent their impact by employing a novel FDDP mechanism to ensure reliable data delivery. The EGA based FDDP model integrates dual objectives. Node parameters like minimal hops, minimal energy consumption, high connectivity, and availability are utilized in the model to determine the optimal dual-disjoint forwarding routes while avoiding malicious nodes. In this system, the FDDP operates using a logical AND gate configuration, with the second path remaining in a standby condition and activated as an alternate forwarding path in case of node failure or malicious node detection. This approach enhances overall transmission reliability and efficiency to meet the demands of wireless sensor networks.
3.1.1 Maintaining low-hop counts
The proposed model aims to achieve QoS-centric and energy-efficient WSN routing by maintaining low hop counts to ensure high connectivity and availability for reliable transmission. Unlike traditional distance-based shortest path models that prioritize minimum hop counts, the model utilizes EC (specifically, the EGA) to explore node and network parameters and generate a set of paths with optimal connectivity, availability, and minimal shared components. This approach involves pruning the complete set of paths to form paths from the source to the destination in a graph. While the Dijkstra algorithm typically increases path lengths by adding new hops to neighboring nodes, the proposed approach considers all connecting nodes for forwarding path selection, especially when forming multiple paths. During pruning, if multiple paths converge at the same intermediate sensor node, only the two best forwarding paths are selected, while the others are removed. By selecting the best forwarding path with improved connectivity and hop counts, the proposed approach enhances reliability and energy efficiency compared to the classical Dijkstra algorithm. Additionally, it effectively reduces the search space, thereby decreasing overall computation and associated energy consumption.
3.1.2 Ensuring minimum shared components
To ensure reliable data delivery in the face of random node death or link loss, the proposed EC-assisted FDDP model focuses on obtaining two-disjoint routes with maximum availability and minimal connectivity loss. The key emphasis is on leveraging node and network-link availability to achieve this objective. After performing shortest path planning or topological optimization, the Evolutionary Genetic Algorithm aims to identify paths with minimal shared components and cost, as lower shared components indicate lower cost. Due to the probabilistic nature of link availability in WSNs, the total path availability cannot be accurately predicted based solely on the availability of connected sensor nodes. To address this, a first-order approximation concept is applied to estimate path and node unavailability. In the proposed method, a Genetic Algorithm is utilized as a heuristic algorithm to identify the best two disjoint paths with minimal connectivity loss, high availability, and minimal or no shared components. Simulations are conducted using the Monte Carlo method to estimate dynamic topology and network conditions, including uncertainties. This approach enables robust routing decisions in WSNs by considering probabilistic network characteristics and uncertainties.
3.2 Model deployment using Bayesian network
The proposed model leverages dynamic node parameters, including node and network availability and connectivity, to optimize forwarding path selection while safeguarding against malicious nodes. Availability denotes the duration a node and its corresponding link remain active, while connectivity signifies the duration a node stays connected to peers or other nodes. Connectivity loss reflects the likelihood of a node disconnecting from its supplementary or alternate forwarding path. Prioritizing higher connectivity and availability facilitates energy-efficient and QoS-centric communication. The model continuously utilizes these parameters to identify optimal forwarding paths, positing that paths with fewer hops exhibit greater link availability and connectivity, thus supporting reliable transmission. Additionally, the model emphasizes minimizing shared components in FDDP to enhance reliability across WSNs. To achieve these objectives, the model employs an EC approach, specifically a Genetic Algorithm, to optimize forwarding path selection and routing decisions for reliable communication in WSNs.
In deploying the WSN network, the model accounts for the probabilistic nature of node behavior by adopting Bayesian principles. It constructs a directed acyclic graph where each connected node represents a random variable. Direct links are established to facilitate the calculation of combined probability distributions, obtained as the product of each node's conditional probability in the graph, thereby forming a Bayesian network. The deployed WSN network can be a hierarchical network with multiple layers containing sensor nodes, links, branches, paths, and connectivity. Noticeably, in the deployed network, the term called "Node and/or allied Link" signifies that the variable about a node can only be one when available or able to communicate. Suppose a node is not available to make communication. In that case, it is labeled as "0" in the Bayesian network model. "Branch" states that a node in Bayesian network deployment can be "1" only when the connected nodes and allied links are available, else it is labeled as "0". Similarly, "Path" signifies that each corresponding sensor node is liable to provide a reliable path connecting the source to the best forwarding paths generated. The other layer of the Bayesian network, "Connectivity," states the connectivity between the selected nodes to constitute the best forwarding path. In such network deployment, one assumption always prevails that the availability of a sensor node is always independent of the other.
Similarly, the availability of a link is always independent of others. In the proposed model, the likelihood of the first layer is characterized by the availability of each node or link. Path availability or link availability can be calculated by considered the formula $\mathrm{L}=\arg \min c(\mathrm{~L})$, where L is the link availability and $\mathrm{C}(\mathrm{L})$ is the cost function used for each path. On the contrary, the 2nd and 3rd layers hypothesize a deterministic model signifying any connection or path can work only when its connected sensor nodes function. In other words, a path can work only when its conditional probability is 1 . In this manner, the proposed routing model obtains the path variables. The $4^{\text {th }}$ layer of the Bayesian model variable signifies the service state of the node, signifying 1 when the node is connected to the forwarding path or not (i.e., 0). Thus, with respective conditional probability values, obtained the node connectivity and availability information, which has been later employed to obtain the link-outage probability to obtain FDDP as an optimal routing solution. Though the deployed network being probabilistic avoids deriving any sophisticated algorithm development for link connectivity and availability estimation, however considering an optimal knowledge transfer, a snippet of the mathematical approach involved is given in the subsequent sections.
To perform data transfer, the proposed model aims to obtain an optimal set of the best forwarding path R connecting the source sensor node n0 to the destination $\mathrm{n}_{\mathrm{f}}$. This path consists of a sequence of nodes $\mathcal{N}=\left\{n_0 \ldots \ldots . n_{\mathrm{f}}\right\}$ and their corresponding link availability and quality, $\delta=$ $\left\{\mathrm{e}_{0,1}, \ldots \ldots \mathrm{e}_{\mathrm{f}-1, \mathrm{f}}\right\}$. Here, $\mathrm{e}_{\mathrm{i}, \mathrm{i}+1}$ shows the communicating path between a node $n_i$ and adjucent node $n_{i+1}$. As mentioned previously, an optimal path can only be established when all connected sensor nodes are available, and their respective links are present (i.e., equal to "1"). Therefore, the available path can be obtained as following Eq. (1):
$\mathbb{A}_r(\mathcal{P})=\prod_{i=0}^{\mathrm{f}} \mathbb{A}_{\mathrm{n}}\left(\mathrm{n}_{\mathrm{j}}\right) \prod_{\mathrm{k}=0}^{\mathrm{f}-1} \mathbb{A}_{\mathrm{e}}\left(\mathrm{e}_{\mathrm{k}, \mathrm{k}+1}\right)$ (1)
With (8), the paths that are unavailable can be calculated using (2).
$\begin{aligned} & \mathrm{U}_{\mathrm{r}}(\mathcal{P})=1-\mathbb{A}_{\mathrm{r}}(\mathcal{P}) =1-\prod_{\mathrm{i}=0}^{\mathrm{f}} \mathbb{A}_{\mathrm{n}}\left(\mathrm{n}_{\mathrm{j}}\right) \prod_{\mathrm{k}=0}^{\mathrm{f}-1} \mathbb{A}_{\mathrm{e}}\left(\mathrm{e}_{\mathrm{k}, \mathrm{k}+1}\right)\end{aligned}$ (2)
Given the current conditions of WSNs where more powerful battery solutions or permanently connected power sources result in reduced link or node unavailability, we can consider using a "First-Order Approximation (FOP)" to estimate node or link unavailability. When used far from the point of linearization, in systems with significant nonlinearities, or in the presence of significant disturbances, FOP may result in errors even if it provides a straightforward and computationally efficient method. By avoiding unavailability in Eq. (2), we can obtain node or link unavailability as follows:
$\begin{gathered}\mathrm{U}_{\mathrm{r}}(\mathcal{P})=1-\prod_{\mathrm{j}=0}^{\mathrm{f}}\left(1-\mathrm{U}_{\mathrm{n}}\left(\mathrm{n}_{\mathrm{j}}\right)\right) \quad \prod_{\mathrm{k}=0}^{\mathrm{f}-1}(1- \left.\mathrm{U}_{\mathrm{e}}\left(\mathrm{e}_{\mathrm{k}, \mathrm{k}+1}\right)\right) \approx \sum_{\mathrm{j}=0}^{\mathrm{f}} \mathrm{U}_{\mathrm{n}}\left(\mathrm{n}_{\mathrm{j}}\right)+\sum_{\mathrm{k}=0}^{\mathrm{f}-1} \mathrm{U}_{\mathrm{e}}\left(\mathrm{e}_{\mathrm{k}, \mathrm{k}+1}\right)\end{gathered}$ (3)
Eq. (3) presents an additive unavailability model, where the cumulative impact of introducing a supplementary node increases unavailability of the added node or corresponding link. This model is considered more reliable than classical non-additive models. In the additive model, the unavailability of the entire path or network is calculated by summing up the individual unavailabilities of each node or link along the path. This provides a more comprehensive understanding of the overall unavailability, taking into account the combined impact of multiple nodes or links being unavailable. This additive approach is advantageous because it captures the cumulative effect of node or link unavailability, providing a more accurate representation of the network's reliability. Additionally, it allows for easier analysis and prediction of network performance under varying conditions.
Node connectivity represents the probability of one forwarding path from the source to the sink is available. Specifically, a node is considered connected to the forwarding path only when it is linked to the initial node and at least one path connecting source to destination is active or available. To assist QoS-centric reliable transmission, each transmitter node constitutes two disjoint forwarding paths. Noticeably, it intends to form dual disjoint paths with minimum or no shared component(s). and at least one path connecting the source to the destination is active or available. To facilitate QoS-centric reliable transmission, each transmitter node establishes two disjoint forwarding paths. Notably, the objective is to create dual disjoint paths with minimal or no shared components. This approach enhances network robustness by ensuring redundancy and resilience in data transmission, thereby improving overall reliability and quality of service.
Let the forwarding paths for a transmitting sensor node $\mathrm{n}_0$ be $\mathcal{P}_0, \ldots \ldots . \mathcal{P}_{\mathrm{K}-1}$ and $\overline{\mathcal{P}_{\mathrm{k}}}$ be the links from $\mathcal{P}_{\mathrm{k}}$. Thus, the connection path can be defined as (4).
$\mathrm{C}\left(\mathrm{n}_0\right)=\mathbb{A}\left(n_0\right) \mathbb{A}\left(\mathrm{U}_{k=0}^{K-1} \overline{\mathcal{P}_k}\right) \mathbb{A}(C)$ (4)
In Eq. (4), the second term represents the availability of the set of sub-forwarding paths. Even if the terminal node is active, the transmitting node $\mathrm{n}_0$ would still be unreachable if the routes $\overline{\mathcal{P}_{\mathrm{k}}}$ fail. Considering this condition, and assuming that node and corresponding link failures are independent in nature, the availability is estimated as shown in Eq. (5). Eq. (5) takes into account the possibility of both node and link failures affecting the availability of the forwarding paths, providing a more comprehensive assessment of the overall network reliability.
$\mathrm{C}\left(\mathrm{n}_0\right)=\mathbb{A}\left(n_0\right) \mathbb{A}\left(\mathrm{U}_{k=0}^{K-1} \overline{\mathcal{P}_k}\right) \mathbb{A}(C)$ (5)
Let $\left\{\mathrm{n}_{\mathrm{k}, 0}, \ldots \ldots \ldots . \mathrm{n}_{\mathrm{k}}, \mathrm{f}_{\mathrm{k}}\right\}$ be the sensor nodes and their allied links in path $k$ be $\left\{\mathrm{e}_{\mathrm{k}, 1,2} \ldots \ldots, \mathrm{n}_{\mathrm{k}}, \mathrm{f}_{\mathrm{k}-1}, \mathrm{f}_{\mathrm{k}}\right\}$ with condition ($\mathrm{n}_{\mathrm{k}, 0}=\mathrm{n}_0 \mathrm{y}_{\mathrm{n_k}}, \mathrm{f}_{\mathrm{k}}=\mathrm{C}$), the node and allied link unavailability are obtained using (6).
$\begin{aligned} & U_r {\left(\overline{\mathcal{P}_k}\right)} =1-\mathbb{A}_r\overline{\left(\mathcal{P}_k\right)=1-\prod_{i=1}^{f_{k-1}} \mathbb{A}_n\left(n_{k, i}\right) \prod_{j=0}^{f_{k-1}} \mathbb{A}_e}\left(e_{k, j ; j+1}\right)\end{aligned}$ (6)
Applying (4)-(6), the eventual connectivity for a transmitter node $\mathrm{n}_0$ is estimated (7).
$\begin{gathered}C\left(n_0\right)=\mathbb{A}\left(n_0\right) \mathbb{A}(C) \times\left(1-\prod_{k=0}^{K-1}(1-\prod_{i=1}^{f_{k-1}} \mathbb{A}_n\left(n_{k, i}\right) \prod_{j=0}^{f_{k=1}} \mathbb{A}_e\left(e_{k, j, j+1}\right))\right)\end{gathered}$ (7)
Noticeably, the proposed EC model utilizes this information or analyzes these node statistics to derive optimal dual disjoint forwarding paths with minimal or no shared components for routing decisions. Initially, the proposed model assesses shared components (or nodes shared across multiple paths from source to destination) to accomplish this. A snippet of the shared component estimation is provided below.
3.2.1 Shared component estimation
Node-connectivity with disjoint nature can be achieved by decoupling the significance of the shared components and corresponding links. Let $\mathcal{R}_0$ and $\mathcal{R}_1$ be the two forwarding paths. Then the connectivity is estimated.
$\begin{gathered}L\left(n_0\right) \approx \sum_{j \epsilon \Phi_n}^f U_n\left(n_j\right)+\sum_{k \in \Phi_e}^{f-1} U_e\left(e_{k, k+1}\right)+ \left(\sum_{i \in \Phi_{n, 0}} U_n\left(n_{0, i}\right)+\sum_{j \in \Phi_{e, 0}} U_e\left(e_{0, j, j+1}\right)\right) \times \left(\sum_{i \epsilon \Phi_{n, 1}} U_n\left(n_{1, i}\right)+\sum_{j \in \Phi_{e, 1}} U_e\left(e_{1, j, j+1}\right)\right)\end{gathered}$ (8)
In (8), $\Phi_{\mathrm{n}}$ and $\Phi_{\mathrm{e}}$ present the sets of shared components, while the non-shared features are $\Phi_{\mathrm{n}}$, and $\Phi_{\mathrm{e}, \mathrm{i}}$ (in path i). Now, employing 1st -order approximations in terms of unavailability, obtain the connectivity loss (9).
Now, realizing the fact that the non-shared links typically do not impact the loss probability causing packet drop or retransmission probability, it is estimated as (11).
$L L\left(n_0\right) \approx \sum_{j \in \Phi_n}^f U_n\left(n_j\right)+\sum_{k \in \Phi_e}^{f-1} U_e\left(e_{k, k+1}\right)$ (9)
Upon reviewing Eqs. (10) and (11), it becomes evident that in the proposed EC model, a dependable source-destination pair naturally possesses dual-disjoint forwarding paths, without necessitating the utilization of any shared components. The approach employed by the EC model, based on GA, focuses on making routing decisions exclusively within clusters of sensor nodes exhibiting minimal connectivity loss probability. This algorithm, termed EC-GA, optimizes network performance by treating connectivity loss probability (CLP) as the primary objective or fitness function. Consequently, paths characterized by the lowest connectivity loss probability are prioritized as feasible candidates for FDDP. A comprehensive exposition on the EC-FDDP model and its network optimization strategies is elaborated in subsequent sections.
3.2.2 EGA based FDDP and network optimization
As detailed in preceding sections, the proposed EGA-FDDP model leverages the link-connectivity and availability parameters discussed earlier to determine an optimal set of FDDP for reliable data transmission. The EC model employs the link-connectivity loss parameter as a cost function, serving as its objective function in identifying suitable forwarding paths. By exploring the search space encompassing all feasible paths, the EC model aims to derive FDDP configurations with minimal or no shared components. This iterative process entails continually refining FDDP by introducing additional hop sensor nodes and evaluating their connectivity probability values. Iterations persist until the likelihood of discovering superior routes diminishes significantly.
The targeted optimization of the network unfolds in two phases: FDDP route selection and pruning. With each iteration indexed by k, identifying a dependable path entails the elimination of alternative paths from S_k, prioritizing those exhibiting low-cost features in terms of connectivity and availability. Consequently, this approach not only facilitates QoS-centric routing but also mitigates computational overhead and conserves energy resources. The proposed EC-based model achieves this optimization by estimating a function termed "Cost-Function c(P)" for every potential path P. Subsequently, the optimal set of paths is determined leveraging Eq. (10).
$L \mathcal{P}^*=\arg \min _R c(\mathcal{P})$ (10)
To estimate the cost function $c(\mathcal{P})$, we begin by considering $\overline{\mathcal{P}}$ as one of the connecting links or forwarding paths formed by extending R, an incomplete route, with a suitable zero-unavailability connection. It's noteworthy that path R terminates at node $n_f$ in this configuration. For any complete forwarding path $M_i \in S_k$, let $L\left(\overline{\mathcal{P}}, M_i\right)$ denote the connectivity loss for the source node $n_0$. Then, the average connectivity loss can be calculated using Eq. (11):
$\tilde{L}(\mathcal{P})=\frac{1}{N_c} \sum_{i=1}^{N_c} L\left(\overline{\mathcal{P}}, M_i\right)$ (11)
In a dynamic network scenario, where the link-loss increment may be inevitable for a path $\mathcal{P}$, we reformulate the cost function as follows
$c(\mathcal{P})=\tilde{L}(\mathcal{P})+E(\mathcal{P})$ (12)
Interestingly, the second component $E(\mathcal{P})$ in Eq. (13) is calculated using the average loss per connection over all path pairs:
$E(\mathcal{P})=\frac{1}{N_c} \sum_{i=1}^{N_c} E\left(\mathcal{P}, M_i\right)$ (13)
where,
$E\left(\overline{\mathcal{P}}, M_i\right)=\frac{\tilde{L}\left(M_i\right)}{\lambda} d\left(n_{\mathcal{P}}, n_f\right)$ (14)
To obtain distance values, we utilize a graph matrix A with components $a_{i j}$, where $a_{i j}=1$ when the relation between node i and node j is active, otherwise $a_{i j}=0$ and $a_{i i}=1$. Using these conditions, we construct a matrix $B(k)$ as shown in Eq. (15):
$B(k)=\mathbb{A}^k$ (15)
where, $B(k)$ has components $b_{i j}(k)$, which represent the total number of paths to get from node i to node j with less than k hops. If $b_{i j}(k)=0$, it indicates that there is no feasible path from i to j in k hops. Therefore, we obtain the shortest path from node i to node j using Eq. (16):
$d(i, j)=\min _{b_{i j}(k)>0}\{k\}$ (16)
Eq. (16) implies that the cost of d(i,j) is the smallest value of hops k with $b_{i j}(k)$>0.
Step 1: Chromosome and Population Initialization
In the Genetic Algorithm representation of the sensor network chromosome, each chromosome is encoded as a string of numbers corresponding to the sensor nodes. The length of each chromosome is determined by the maximum number of sensor nodes in the path direction. In our proposed model, the sensor nodes are enumerated as n1, n2, ..., nf, denoted by the set N. Initially, the population is initialized with each chromosome representing a valid path. The positions of nodes play a crucial role in constructing the initial routing, achieved through population initialization. A list, Np, is created initially, containing all one-hop neighbors q→p, linking every $q \in\mathrm{~Np}$ to transmit data from the source node p to the destination (base station) through q. This information is then utilized to generate the initial populations by randomly selecting the next-hop node $q \in\mathrm{~Np}$ for each node p to design potential routes, i.e., chromosomes.
Step 2: Fitness Function
After the formation of new individuals, the fitness value for each chromosome must be calculated, as it plays a vital role in the selection process to form a mating pool. The fitness value is determined based on the lifetime of the sensor network, treated as a cost function C(P). For individual excellence, the fitness function is defined as follows (Eq. (17)):
$\mathcal{P}^*=\arg \min _R c(\mathcal{P})$ (17)
To achieve this, our proposed EC-based model estimates a function called the "Cost-Function C(P)" for each possible path P. Consequently, the optimal set of paths is obtained by utilizing this function. The following mechanism is introduced to estimate the cost function C(P). Consider $\mathcal{P}^*$ to be one of the connecting links or forwarding routes, an incomplete route via an efficient zero-unavailability relation, formed by extending R. Notably, in this configuration, the path R is connected to the node $n_f$.
Step 3: Selection and Crossover
The selection of individuals is performed using roulette wheel selection to construct the mating pool. Individuals with more advantageous characteristics within the context of the roulette wheel have a higher probability of being selected. In this process, the uniform crossover operator is employed to generate new offspring. Through the mutation of two parents, a pair of offspring is produced via standardized crossover, with the expectation that they will exhibit improved fitness compared to their parents.
Step 4: Mutation
To address the issue of premature convergence, the genetic diversity of the population is maintained through mutations. During mutation, the pth gene is altered by a neighboring node of node Ni, ensuring that the individuals remain valid.
Step 5: Elicit Genetic Algorithm for Routing
The model implements an Elicit genetic algorithm for routing in WSNs. The Elicit GA incorporates Elicit by dividing the mating pool into two groups: Group-1 and Group-2. Group-1 comprises 20% of individuals with the highest fitness advantages, including copies for subsequent generations. Group-2 consists of the remaining 80% of individuals. Additionally, 10% of individuals are randomly generated as mutants for the next generation.
In the Elicit Genetic Algorithm, the parameterized uniform crossover operator is employed, to generate offspring. This crossover operator randomly selects the first parent from Group-1 (Smallest Group) and the second parent from Group-2 (Largest Group). Elicit is integrated into the Elicits GA to preserve the best individuals from one generation to the next, ensuring that the fittest individuals are consistently enhanced across successive generations.
The EGA-FDDP model introduced in this study leverages node and link availability and connectivity to establish innovative dual-disjoint forwarding paths (FDDP). Its primary aim is to achieve dual-disjoint path selection while ensuring enhanced connectivity, minimal hop counts, and minimal or no-shared components. There is a strong emphasis on maintaining low hop counts to decrease the probability of drop or link-outage, ensuring successful data delivery to the destination node even in scenarios of potential connection failure or node loss, without necessitating retransmission or iterative node discovery.
In contrast to prior studies relying on conventional distance parameters such as Dijkstra or Euclidean distance, the proposed model employs the Elitist Genetic Algorithm (EGA), a form of EC algorithm, to establish optimal FDDP based on information regarding link availability and connectivity. This methodology aims to provide both QoS assurance and energy efficiency. The NS2 architecture platform is employed for implementing the proposed WSN routing model. To assess the of the proposed EGA-FDDP compared to a recently proposed EC approach known as Cuckoo Search and Harmony Search (HS) based routing protocol for WSNs, we conducted evaluations of both methods. While the EGA-FDDP focuses on achieving optimal forwarding paths with minimal hop counts and ensuring data delivery without retransmission, the Enhanced Cuckoo Search and HS-based routing protocol primarily target energy efficiency by identifying optimal forwarding nodes and paths in multi-hop transmission scenarios.
The performance of the proposed model is based on the EC concept evaluated in terms of throughput, data loss, energy consumption, and delay. The results obtained from NS2-based simulated outputs were further analyzed using MATLAB, as illustrated in Figures 1 to 4. The proposed model was implemented using the NS2 development platform with specific simulation variables and experimental setup values, including a network size of 49 nodes deployed over a WSN dimension of 100x100, IEEE 802.15.4 Mac and PHY protocols, radio signal range, carrier frequency, antenna specifications, and various other parameters. Figure 1 demonstrates the throughput variation between the proposed routing protocol and different existing mechanisms. The proposed model consistently achieved higher throughput (96-98%) even with increasing network size compared to GA, EGA, and iCSHS.
Figure 1. Node density vs throughput
Figure 2. Node density vs packet loss rate
Figure 2 shows the packet loss rate comparison the proposed routing protocol and different existing mechanisms like GA, EGA, iCSHS. Packet loss was significantly reduced in the proposed model, attributed to the avoidance of malicious nodes in the forwarding path and the selection of paths based on parameters such as high node availability and link availability.
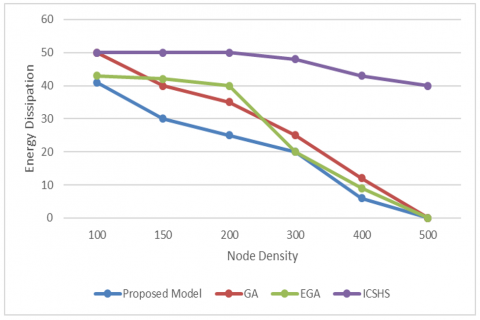
Figure 3. Node density vs energy dissipation
Figure 3 displays the energy consumption comparison the proposed routing protocol and different existing mechanisms like GA, EGA, iCSHS. The proposed model exhibits lower energy consumption due to its low computational complexity compared to iCSHS.
The proposed model exhibits lower energy consumption due to its low computational complexity compared to few existing mechanisms Figure 4 shows the comparison of end to end dalay of the proposed model and the existing three mechanisms like GA, EGA, and ICSHS.
Figure 4. Node density vs delay
Overall, the proposed EGA-FDDP paradigm demonstrated better reliability, higher transmission success rate, lower energy consumption, and reduced end-to-end delay compared to GA, EGA, iCSHS. These attributes make the proposed system well-suited for contemporary WSN-based communication systems.
This research paper presents the development of a novel EC algorithm termed EGA. The algorithm aims to enhance fault resilience and energy efficiency in WSNs. The main goal of this study is to utilize network and node connectivity, as well as link availability, for dual disjoint path estimation. The method, named EGA-based FDDP selection, is devised to enable dependable and QoS-focused communication across WSNs. This strategy underscores the probabilistic nature of WSNs and seeks to identify two optimal forwarding paths with minimal shared components, thereby reducing computational overhead while ensuring robust reliability and QoS provisioning. The proposed model strives to mitigate packet drop probability and retransmissions, ultimately enhancing QoS and energy efficiency. Through the utilization of dynamic network parameters and adaptive routing decisions, the proposed routing approach demonstrates its adaptability. Simulations conducted using Network Simulator indicate that the proposed routing protocol outperforms the native IEEE 802.15.4 protocol standard in terms of throughput and packet loss, while maintaining backward compatibility and suitability for real-time routing solutions. Future research could explore spatio-temporal features based on network dynamics and utilize various classifiers or machine learning techniques to leverage the spatial and temporal behavior of nodes for outlier detection. The derived outlier patterns could then be translated into actionable insights to facilitate expedited routing decisions without the need for repeated detection processes.
[1] Chit, T.A., Zar, K.T. (2018). Lifetime improvement of wireless sensor network using residual energy and distance parameters on LEACH protocol. In 18th International Symposium on Communications and Information Technologies (ISCIT), Bangkok, Thailand, pp. 186-190. https://doi.org/10.1109/ISCIT.2018.8587930
[2] Shen, J., Wang, A., Wang, C., Hung, P., Lai, C. (2017). An efficient centroid-based routing protocol for energy management in WSN-assisted IoT. IEEE Access, 5: 18469-18479. https://doi.org/10.1109/ACCESS.2017.2749606
[3] Razzaq, M., Ningombam, D., Shin, S. (2018). Energy efficient K-means clustering-based routing protocol for WSN using optimal packet size. In International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, pp. 632-635. https://doi.org/10.1109/ICOIN.2018.8343195
[4] Istwal, Y., Verma, S. (2017). Dual cluster head routing protocol in WSN. In 8th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Delhi, India, pp. 1-6. https://doi.org/10.1109/ICCCNT.2017.8203940
[5] Sari, A., Caglar, E. (2018). Load balancing algorithms and protocols to enhance quality of service and performance in data of WSN. In Security and Resilience in Intelligent Data-Centric Systems and Communication Networks, pp. 143-178. https://doi.org/10.1016/B978-0-12-811373-8.00007-0
[6] Liu, Y., Wu, Q., Zhao, T., Tie, Y., Bai, F., Jin, M. (2019). An improved energy-efficient routing protocol for wireless sensor networks. Sensors, 19(20): 4579. https://doi.org/10.3390/s19204579
[7] Roshini, A., Kiran, K. (2023). Hierarchical energy efficient secure routing protocol for optimal route selection in wireless body area networks. International Journal of Intelligent Networks, 4: 19-28. https://doi.org/10.1016/j.ijin.2023.01.002
[8] Tretyakova, A., Seredynski, F. (2012). Evolutionary algorithm-based solutions to maximum lifetime coverage problem in wireless sensor networks. In 2012 2nd IEEE International Conference on Parallel, Distributed and Grid Computing, Solan, India, pp. 174-179. https://doi.org/10.1109/PDGC.2012.6449812
[9] Darji, H., Shah, H.B. (2016). Genetic algorithm for energy harvesting-wireless sensor networks. In 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, pp. 1398-1402. https://doi.org/10.1109/RTEICT.2016.7807992
[10] Hu, T., Fei, Y. (2010). QELAR: A machine-learning-based adaptive routing protocol for energy-efficient and lifetime-extended underwater sensor networks. IEEE Transactions on Mobile Computing, 9: 796-809. https://doi.org/10.1109/TMC.2010.45
[11] Firdous, S., Bibi, N., Wahid, M., Alhazmi, S. (2022). Efficient clustering based routing for energy management in wireless sensor network-assisted Internet of Things. Electronics, 11(23): 3922. https://doi.org/10.3390/electronics11233922
[12] Zaman, K., Sun, Z., Hussain, A., Hussain, T., Ali, F., Shah, S.M., Rahman, H.U. (2023). EEDLABA: Energy-efficient distance-and link-aware body area routing protocol based on clustering mechanism for wireless body sensor network. Applied Sciences, 13(4): 2190. https://doi.org/10.3390/app13042190
[13] Bhushan, S., Pal, R., Antoshchuk, S.G. (2018). Energy efficient clustering protocol for heterogeneous wireless sensor network: A hybrid approach using GA and K-means. In 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, pp. 381-385. https://doi.org/10.1109/DSMP.2018.8478538
[14] Shimly, S.M., Smith, D.B., Movassaghi, S. (2019). Experimental analysis of cross-layer optimization for distributed wireless body-to-body networks. IEEE Sensors Journal, 19(24): 12494-12509. https://doi.org/10.1109/JSEN.2019.2928235
[15] Kreibich, O., Neuzil, J., Smid, R. (2014). Quality-based multiple-sensor fusion in an industrial wireless sensor network for MCM. IEEE Transactions on Industrial Electronics, 61(9): 4903-4911. https://doi.org/10.1109/TIE.2013.2297316
[16] Hendriks, T., Camelo, M., Latré, S. (2018). Q²-routing: A QoS-aware Q-routing algorithm for wireless ad hoc networks. In Proceedings of the 14th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Limassol, Cyprus, pp. 108-115. https://doi.org/10.1109/WiMOB.2018.8589162
[17] Vinodhini, R., Gomathy, C. (2020). MOMHR: A dynamic multi-hop routing protocol for WSN using heuristic-based multi-objective function. Wireless Personal Communications, 111: 883-907. https://doi.org/10.1007/s11277-019-06815-w
[18] Khan, F., Memon, S., Jokhio, S.H. (2016). Support vector machine-based energy-aware routing in wireless sensor networks. In Proceedings of the 2nd International Conference on Robotics and Artificial Intelligence (ICRAI), Rawalpindi, Pakistan, pp. 1-4. https://doi.org/10.1109/ICRAI.2016.7791236
[19] Gu, X., Zhou, X., Yuan, B., Sun, Y. (2018). A Bayesian compressive data gathering scheme in wireless sensor networks with one mobile sink. IEEE Access, 6: 47897-47910. https://doi.org/10.1109/ACCESS.2018.2867538
[20] Singh, K., Kaur, J. (2017). Machine learning-based link cost estimation for routing optimization in wireless sensor networks. Advanced Wireless and Mobile Communication, 10: 39-49.
[21] Masoud, M. Z., Jaradat, Y., Jannoud, I., Al Sibahee, M. A. (2019). A hybrid clustering routing protocol based on machine learning and graph theory for energy conservation and hole detection in wireless sensor network. International Journal of Distributed Sensor Networks, 15: 1550147719858231. https://doi.org/10.1177/1550147719858231
[22] Murudkar, C.V., Gitlin, R.D. (2019). Optimal-capacity, shortest path routing in self-organizing 5G networks using machine learning. In Proceedings of the 20th Wireless and Microwave Technology Conference (WAMICON), Cocoa Beach, FL, USA, pp. 1-5. https://doi.org/10.1109/WAMICON.2019.8765446
[23] Hendriks, T., Camelo, M., Latré, S. (2018). Q2-routing: A QoS-aware Q-routing algorithm for wireless ad hoc networks. In 2018 14th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Limassol, Cyprus, pp. 108-115. https://doi.org/10.1109/WiMOB.2018.8589161
[24] Vimalapriya, M., VigneshBaalaji, S., Sandhya, S. (2019). Energy-centric route planning using machine learning algorithm for data-intensive secure multi-sink sensor networks. International Journal of Innovative Technology and Exploring Engineering, 9: 4866-4875.
[25] Yang, J., He, S., Xu, Y., Chen, L., Ren, J. (2019). A trusted routing scheme using blockchain and reinforcement learning for wireless sensor networks. Sensors, 19(4): 970. https://doi.org/10.3390/s19040970
[26] Yao, H., Yuan, X., Zhang, P., Wang, J., Jiang, C., Guizani, M. (2019). A machine learning approach of load balance routing to support next-generation wireless networks. In Proceedings of the 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, pp. 1317-1322. https://doi.org/10.1109/IWCMC.2019.8766698
[27] Ghaffari, A. (2017). Real-time routing algorithm for mobile ad hoc networks using reinforcement learning and heuristic algorithms. Wireless Networks, 23: 703-714. https://doi.org/10.1007/s11276-016-1196-9
[28] Strykhaliuk, B., Kolodiy, R., Faichuk, V. (2019). Method for intelligent routing within ad-hoc networks with complex topology. In Proceedings of the 3rd International Conference on Advanced Information and Communications Technologies (AICT), Lviv, Ukraine, pp. 340-343. https://doi.org/10.1109/AIACT.2019.8847761
[29] FatemiAghda, S.A., Mirfakhraei, M. (2019). An improved cluster routing protocol to increase the lifetime of wireless sensor network (WSN). Wireless Personal Communications, 109(3): 2067-2075. https://doi.org/10.1007/s11277-019-06678-1
[30] Hammoudeh, M., Newman, R. (2015). Adaptive routing in wireless sensor networks: QoS optimization for enhanced application performance. Information Fusion, 22: 3-15. https://doi.org/10.1016/j.inffus.2013.02.005
[31] Rodrigues, P., John, J. (2020). Joint trust: An approach for trust-aware routing in WSN. Wireless Networks, 26: 3553-3568. https://doi.org/10.1007/s11276-019-02079-1