A Compact Dielectric Resonator Antenna Based Microwave Sensor for Non-Invasive Blood Glucose Monitoring

Diabetes is a long-term metabolic disorder with an inability to produce sufficient insulin or an inability to use insulin by the body effectively. The International Diabetes Federation (IDF) estimates that 700 million adults will have diabetes worldwide by 2045 [1]. Diabetes is an ever-more serious issue for healthcare systems globally and is ranked among the great health emergencies of the twenty-first century. In India, in particular, the second-largest population of adults in the world, approximately 77 million are suffering from diabetes. Furthermore, diabetes and its complications are the primary cause of death related to diabetes in South-East Asia, resulting in an estimated one million deaths per year [2]. Successful diabetes management, which is usually accomplished through the main objectives of health systems, calls for frequent monitoring of blood glucose. The pain and discomfort of the procedure usually discourage patients from proceeding with monitoring, potentially weakening disease control. Access to good quality diabetes care is one of the main objectives of health systems [3]. Yet, the rise in prevalence of the disease and the substantial expense of long-term care are putting pressure on the healthcare industry. To handle these challenges, the six basic pillars of healthcare systems need to be improved: management, information systems, access to healthcare, human resources, and delivering services. Non-invasive glucose monitoring devices present a strong substitute in this regard. These technologies offer benefits in terms of patient compliance, portability, ease of use, and user comfort when compared to conventional methods [4]. Antenna-based sensing systems, particularly DRAs, have garnered interest among emerging non-invasive technologies due to DRAs, have garnered interest among the new non-invasive technologies because of their high sensitivity and efficiency at millimeter-wave and microwave frequencies [5-8].  Due to these qualities, they are now used in military radar technologies and small wireless communication systems [9]. In this research, we explore a novel application of DRAs for non-invasive glucose monitoring by leveraging their resonance behavior to detect changes in the dielectric properties of biological tissues that correlate with fluctuations in blood glucose levels. Any change, such as modifications in the electrostatic characteristics of adjacent tissue, can cause the resonant frequency of DRAs to shift. DRAs resonate at particular microwave frequencies. Since these changes can be linked to changes in blood glucose levels, this characteristic makes DRAs attractive options for non-invasive glucose sensing.

Table 1. Comparison of non-invasive microwave glucose monitoring sensors

Changes in glucose levels can be detected using these designs, which leverage the sensitivity of resonant frequency shifts to changes in tissue permittivity. Table 1 presents a comparative analysis of the sample microwave sensors provided in the literature. Although many of these methods show promise in terms of resolution, they often have drawbacks, such as being bulky, inefficient, or causing significant losses in biologically interactive several advantages, including DRAs have a number of advantages, such as small dimensions, excellent radiation efficiency, minimal dielectric loss, and considerable gain; these features are particularly useful for wearable or portable biosensing applications. Motivated by these advantages, the current study presents a cylindrical DRA developed specifically for non-invasive glucose detection in the microwave range.

In order to realistically evaluate the interaction between the proposed antenna and human tissue for non-invasive glucose sensing, a simplified anatomical model of the human thumb was developed and simulated in CST Studio Suite. To evaluate the impact of changes in tissue permittivity, particularly in the blood layer, on the antenna's performance, this EM model is positioned above the dielectric resonator, serving. Nevertheless, the representative biological load. The layered bio-organic materials that comprise human tissue are naturally heterogeneous and exhibit. It employs a layered modeling approach for conceptual clarity and computational efficiency. Despite voxel-based modeling being computationally inefficient, it is frequently used in bio-electromagnetics for high-resolution anatomical simulations. In the context of glucose sensing, the focus is on depicting the pertinent layers that have a major impact on EM wave interaction and propagation. Blood, fat, bone, skin, and nail are the five main layers that comprise the human body model. The estimated average thicknesses found in adult human anatomy are used to model these layers, and that are arranged vertically. The thumb model's overall dimensions of 15 × 25 × 12.3 mm³ provide an accurate scale for near-field antenna interaction.

A key aspect of the simulation is modeling the dielectric response of blood, as its permittivity is known to vary with glucose concentration and frequency. To account for this, the blood layer is represented by means of the Cole-Cole dispersion model, which accurately describes the frequency-dependent behavior of complex permittivity in biological tissues. The remaining layers, skin, fat, bone, and nail, are modeled as homogeneous dielectric materials with fixed permittivity values, based on standard datasets [15, 16]. The structural representation of the 3D EM thumb model is shown in Figure 4, and the detailed EM parameters and thicknesses of each layer are provided in Table 3.

4.png

Figure 4. Detailed view of the 3D EM human thumb model created in CST Studio

Table 3. Thickness and dielectric properties of separate layers in the EM model of the human thumb

To analyze the performance of the proposed CDRA structure for glucose measurement non-invasively, a series of EM simulations were performed using CST Microwave Studio. The simulations were aimed at investigating the impact of the operating frequency of the antenna and the changing levels of glucose in the simulated human blood layer. Under normal conditions (i.e., without the presence of any biological load), the CDRA had a resonant frequency of 4.187 GHz. However, the introduction of the 3D EM human thumb model altered the resonant frequency to around 4.75 GHz. The shift in frequency is illustrated in Figure 6, and it illustrates how the antenna performance is affected by the biological interface. This observation verifies the system's sensitivity to dielectric loading and encourages further research into whether changes in blood permittivity caused by glucose result in measurable and repeatable shifts in resonant frequency.

61.png

Figure 6. Graph illustrating the resonant frequency of DRA with and without thumb

However, in actual use, reliable sensor performance also relies on repeatable and stable thumb placement, which can change between individuals and across trials. To assess this factor, a schematic model of thumb positioning on the x-axis was created and is illustrated in Figure 7. Offsets from the center (0 mm) to ±2 mm replicate real-world variation in user interaction. The effect of these lateral movements on resonant behavior is indicated in Figure 8, which shows the simulated S11 response curves for all displacement cases. Small variations in positioning lead to noticeable oscillations, showing the relevance of precise positioning for reproducible sensing.

7.png

Figure 7. Schematic representation of thumb positioning along the x-axis

Table 6 shows the simulated S-Parameter (S11) values (reflection coefficient) for eight different glucose levels, from 0 to 16,000 milligrams per deciliter. The results show a smooth, nearly linear increase in resonant frequency with an increase in glucose concentration, indicating the possibility of the antenna's application as a dielectric glucose sensor. In order to quantify the performance of the sensor, the sensitivity (S) was determined from the rate of change in the resonant frequency with respect to glucose concentration. Sensitivity is given by:

$\mathrm{S}=\frac{\Delta f_r}{\Delta G}$                    (5)

where $\Delta f_r$ is the change in resonant frequency (in MHz) and $\Delta G$ is the corresponding change in glucose concentration (in mg/dL). From the data in Table 6, the frequency shifts from 4.750 GHz to 4.780 GHz over a glucose concentration range of 0 to 16,000 mg/dL. According to these data points, the sensor's sensitivity is estimated to be 1.87 kHz/mg/dL. This result highlights the antenna’s capability to detect subtle dielectric changes associated with varying glucose levels, affirming its potential for accurate, non-invasive glucose monitoring. To further investigate the sensitivity of the CDRA to glucose levels, simulations were repeated for various blood layer thicknesses using different Cole–Cole parameter sets. Table 7 shows the resulting resonant frequencies across multiple glucose concentrations and tissue thickness values.

62.png

Figure 8. The variations of resonant frequency of DRA when thumb is placed in different positions

Table 7. Resonant frequency obtained for various Cole-Cole materials with respect to the blood layer

As expected, increasing the thickness of the blood layer leads to a higher overall shift in resonant frequency, confirming the depth of interaction between the resonator and the target layer. The nearly linear progression of operating frequency with increasing glucose level is further illustrated in Figure 9. This trend supports the hypothesis that the CDRA. can serve as a non-invasive, dielectric-based glucose sensor. Similar frequency-based sensing methods have been investigated in prior research for hydration and tissue monitoring applications [23, 24].

9.png

Figure 9. Graph showing the linear variation of glucose level from 0 (mg / dL) - 16000 (mg / dL) versus resonant frequency

Overall, these results confirm that the CDRA responds sensitively and predictably to changes in glucose concentration within biologically relevant limits. This makes the proposed structure a viable candidate for further development in continuous glucose monitoring applications. However, in real-world scenarios, additional physiological factors such as tissue compression and anatomical variation can influence the effective thickness of biological layers, particularly under pressure from the thumb’s placement on the antenna. Blood layer thickness, for instance, can vary naturally between individuals and dynamically due to applied pressure. This variation can subtly influence the resonant response of the sensor. Table 8 presents the simulation results showing how changes in blood thickness affect the resonant frequency of the antenna.

Table 8. Variation in thumb size due to blood layer thickness

Additionally, variation in nail thickness was investigated, as this superficial layer may differ across individuals. However, simulation results in Table 9 show negligible impact on the resonant frequency, suggesting that nail variability does not significantly influence sensing accuracy. From the data presented in these tables, it can be concluded that variations in skin, blood, or nail thickness, whether due to effect on the resonant behavior of the CDRA. This indicates strong robustness of the proposed antenna design against real world biological variability. anatomical diversity or finger pressure, have only a marginal effect on the resonant behavior of the CDRA. This indicates strong robustness of the proposed antenna design against real world biological variability.

Table 9. Resonant frequency obtained for various Cole-Cole materials with respect to the skin layer

While the Cole–Cole model used in this study enables comprehensive analysis across a wide range of dielectric conditions, the simulated glucose concentrations up to 16,000 mg/dL exceed physiologically realistic levels. This selection was originally made following earlier work [20], which simulated plasma dielectric response over a wide range to test sensor sensitivity and response behavior under theoretical extremes. To further validate the clinical utility of the proposed system, further simulations were performed employing aqueous glucose solutions within a clinically realistic concentration range from 50–250 mg/dL, based on data reported in the researches.

The electric properties of the solutions were derived from experimental data, with the relative permittivity decreasing monotonically and the equivalent conductivity remaining constant with increasing glucose concentration. Table 10 reports the dielectric values employed in this study. Figure 10 illustrates that the S11 demonstrates distinguishable resonant frequency shifts for the various glucose concentrations. These findings further support the sensitivity of the antenna in clinically valuable glucose concentrations and assist in validating the viability of implementing the design in real-world, non-invasive supervision of glucose levels. The estimated sensitivity of aqueous glucose solution is approximately 0.7 MHz/mg/dL. To determine the radiation performance of the CDRA, Fairfield simulations were conducted as well. The proposed antenna has a gain of up to 6.526 dBi and a half-power beamwidth of about 90°, as illustrated in Figure 11 and Figure 12. The excitation of higher-order hybrid modes is responsible for such a performance, generating a directional radiation pattern appropriate for near-field sensing purposes.

Table 10. Electrical properties of aqueous glucose concentrations used for validation

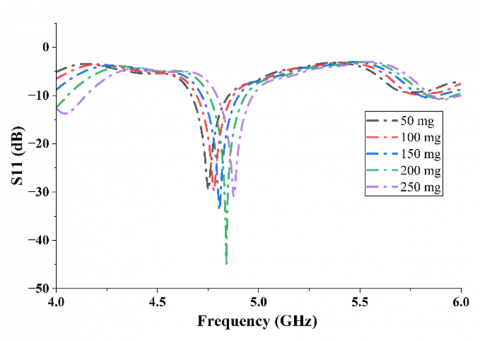
Figure 10. Simulated S11 curves for aqueous solutions of glucose in the 50 (mg / dL) to 250 (mg / dL) range, exhibiting observable frequency shifts with increasing concentration of glucose

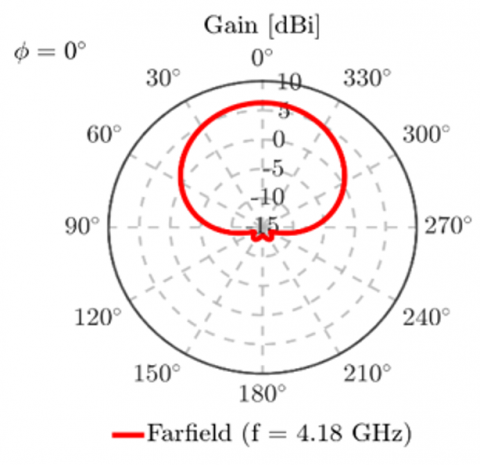
Figure 11. 2D Radiation pattern of the proposed design at $\phi$ = 0⁰

12.png

Figure 12. 2D Radiation pattern of the proposed design at $\phi$ = 90⁰

Directivity of the antenna was computed as 6.964 dBi, which is indicative of having a high main lobe. In addition, side-lobe levels were very low, as can be seen in Figure 12, with the aim of causing negligible unwanted radiation and higher sensitivity along the forward direction. Antenna efficiency $\eta$, which is the ratio of gain (G) to directivity (D), was computed by:

$\eta=\frac{G}{D}=\frac{6.526}{6.964} \approx 0.93$ or $93 \%$                  (6)

This efficiency is very high, which ensures that most of the power delivered to the antenna is radiated properly, a requirement of high-performance biomedical sensors.